|
v.7 No
1 |
3 |
| On conservation of energy
and impulse |

|
VLADIMIR: I’m not against your approach, dear Sergey,
only I’m afraid, is not it the case ‘to swat a fly with a sledgehammer’  .
And see, why. .
And see, why.
You are writing, for relativists the very fact of
translation is of no importance, they are satisfied with the fact that the laws of
dynamics are true in the frame freely falling in the homogeneous gravity field.
I agree, this is of no importance for them, but, as I can
judge, ‘of no importance’ is too delicately said. The task which Einstein
pursued when started his GRT was, as far as I can judge, to lift, to deny, to consign to
oblivion the statement of classical physics that free motion of bodies in space and time
and their same motion under affection of forces are basically different motions. According
to their logic, there is, and can be, no translation between them.
In classical mechanics we consider kinematics and
dynamics. Classical physics cries out “danger!” seeing such theory as SRT –
mere kinematic theory, or rather such which mere mathematically and so ruthlessly approach
the problem of space-time and chisels from them, for beloved itself, the 4-continuum (!)
after definite rules (!), to please its basic postulates. It cries out “danger!”
also because these postulates, as you correctly underline, are kinematic, not dynamic,
though the basic work had the name “On electrodynamics of moving bodies”, –
but just “On…”.  . .
I can be wrong, but it seems to me, here also, breaking
into the gravity fields, they cared more of kinematics than of dynamics, they did not
think of dynamics and, truly speaking, lost it already in SRT. So they had to postulate
such eccentric things as ‘energy-mass translation’ and other
‘wonders’.  . .
SERGEY: I absolutely agree with you.
VLADIMIR: I mean, don’t you think of relativists too
good supposing that they cared, whether the laws of dynamics are true in non-IRFs? Then
why don’t they care that these laws don’t work in SRT? I think, relativists
simply have not the problem of translation from IRF to non-IRF, as their point is
the equivalence of these frames. Having claimed so loudly, they by volition freed
themselves from the necessity to think, how to translate from frame to frame. Everything
for people = everything for me! 
SERGEY: Thus, dear Vladimir, just as I said from the
beginning, the issue, how much legal is the Relativity, is
not in physics but in the plane of clan interests and psychology. You now are
corroborating it.
You are right, of course, saying, it’s impossible to
prove something to relativists. I would add, impossibility follows from the fact that they
long ago made sure, how absurd is their conception. In fact, the situation is like in the
novel “Golden calf” by Ilf and Petrov, when they sawed ‘golden’
dumbell (for English-speaking readers: they have stolen from one millionaire a 16-kg
dumbell, thinking, it is gold):
“– Why! – suddenly said Balaganov and
stopped working. – I saw three hours, and it still is not golden.
Panikovsky did not reply. He already understood and last
half of an hour made an appearance that sawed.
– Well, let’s saw some more! – cheerfully
said golden-haired Shura.
– Of course, we have to saw, – remarked
Panikovsky, trying to postpone the terrible time of reckoning.
He closed the face by palm and through fingers looked at
the rhytmically moving strong spine of Balaganov.
– I cannot understand it! – said Shura, having
sawed to the end and disjoining two halves of ‘apple’. – This is not gold!
– Saw, saw, – babbled Panikovsky.
But Balaganov, having in hands iron hemispheres, slowly
approached the violator of convention.
– Don’t come up to me with this
iron! – squealed Panikovsky, running off. – I despise you!” [p. 191].
Is not it a very common behaviour of relativists? And now,
when people gradually return from the absurd imposed on the science by relativists, a part
of them, not so militant and not having lost the limits in defending of dogma as such,
disappears from the battles without good-bye and finds some other activities. But most
insistent will require, of course, to saw to the end.
Not in them is the problem. This all will gradually calm
down. It is important to understand, how mistaken are the relativistic approaches, lest,
developing the classical formalism for the high speeds and energies, to replicate their
mistakes, as the adherents of aethereal conception do now, thinking that we may partially
change most absurd discrepancies of Relativity and retain the fantasies like photons, time
transforms, wrapping space-time in the aethereal theory, may substitute the dynamical
description of processes by that kinematic, – you say it absolutely right, – and
the crisis of Relativity will be got over. No, until we have not revealed all mistakes and
have not taken off from models all absurd statements and corollaries based on them, the
crisis will go on, producing new and new monsters in new post-relativistic incarnation.
So, with your permission, I would return to the promised
analysis, how legal is it to postulate the equivalence of laws of kinematics and dynamics
in frames of relativistic conception.
Before we start analysing, whether it is legal to think
equivalent the inertial and freely falling frames in the aspect, how the laws of dynamics
work in them, let us reveal the reefs which we will encounter and which we would want to
avoid. The main reef is that in frames of SRT the translation from inertial to
non-inertial frame is not defined formally.
As you remember, in classical formalism we easily made it
kinematically, as neither time nor spatial parameters transformed in translations. And the
main, the lightspeed was not strongly related to each frame and its value we yielded as
the corollary of Galilean transforms. The value of lightspeed could remain same or become
anisotropic, the distribution of equiphase surfaces could change, but this all did not
affect the rest phenomena and material bodies. In other words, though we detect the
phenomena with help of light, the properties of light do not affect physical properties of
other material bodies and the more geometry of space and properties of time. In
Relativity, Einstein’s postulate of constant speed of light is true exceptionally in
IRFs and properties of light have a direct effect on the properties of time, space and
geometrical size of bodies. In case when the bodies in the moving frame are accelerated
differently, to prove this postulate true is impossible. From the classical view, it is
clear, why – because even at small speeds and accelerations the lightspeed in
non-inertial frames will not be constant and Einstein never found ‘evidences’
(when classical ‘obviousness’ is minded but it is realised relativistically).
And he could not find, as in classical formalism there also is no way to this
‘obviousness’ – nothing to copy. Just so, when Einstein encountered the
necessity of accelerated motion, especially with necessity to pass to the accelerated
frame, he ‘distracted’ to some approximations, reducing the accelerated frame to
the frame ‘locally inertial in time’, which, basically, is the trick he multiply
used to interrelate GRT with SRT. Already in his first paper “On electrodynamics of
moving body” Einstein defined the statement of problem of electron’s
acceleration in the external field so: “Let a point particle with an electric charge  (called further
‘electron’) move in the electromagnetic field; of the law of its motion we will
premise only the following.
If the electron rests during some interval
of time, in the nearest next moment of time the motion of electron, as it is slow (! – Sergey) will be described by equations (called further
‘electron’) move in the electromagnetic field; of the law of its motion we will
premise only the following.
If the electron rests during some interval
of time, in the nearest next moment of time the motion of electron, as it is slow (! – Sergey) will be described by equations |
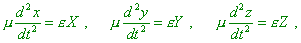 |
(d1.11) |
where x, y, z are the
coordinates of electron and  is the mass of electron. is the mass of electron.
Then, let the electron during some
interval of time to have the speed v (note,
in this statement of problem, the electron has not the momentary speed v, as it is
done in accelerated motion, but some constant speed during though little but interval of
time – Sergey). Find the
law according to which the electron moves in the immediately next element of time after
this interval.
Doing not limiting the generality of
considerations, we can assume, and assume actually, that at the moment when we start the
observation, our electron is in the coordinate origin and moves along the axis X of
the frame K with the speed v. In this case it is clear that at the indicated
moment of time (t = 0), the electron rests relative to the coordinate system k
moving in parallel to the axis X with the constant speed v ” [A. Einstein. On electrodynamics of moving body. –
In: Collection of scientific works, vol. 1, p. 32 (Russian)].
Having read this statement of problem, you hopefully will
agree with me, Einstein’s statement of substitution of momentary speed by some speed
constant in the time interval, as well as confinement to the small speeds and
accelerations, essentially limit the generality. The more they disable to substitute the
accelerated frame by some inertial frame, even at small time interval. And this makes
illegal to apply solutions yielded in this approximation to the sub-light speeds. Even if
solutions are correct, they are applicable only to small speeds. So, when relativists
attempt solving electrodynamic problems for charged bodies at sub-light speeds, they
automatically exceed the limits in which Einstein’s mathematical tool is true and
automatically make their solutions incorrect.
I also think, you already understand, why Einstein dared
to make such step, having substituted the non-inertial frame by that inertial. Yes,
because of vagueness, whether the postulate of constant speed of light remains true in the
accelerated frame. And accelerated not in the homogeneous gravity field but in some
arbitrary electromagnetic field.
Perhaps we should not be caught by this vagueness again,
the more, below we will see, we have no necessity in it.
We can first check the conservation of laws of dynamics in
translation not from IRF to non-IRF but from IRF to IRF. Surely, if Einstein wrote
(d.1.11) in the initial inertial frame as the Newton law and, naturally, premised some
arbitrarily given frame, in this way he premised that in Relativity this law is true in
all relativistic IRFs. Consequently, as the initial point of check, how much correct the
laws of dynamics are in Relativity, we can consider a simple case – a lumped force of
constant magnitude affecting some body with the mass m.
It can outwardly seem that we repeat the problem of
electron’s acceleration, but it is not so. First of all, in the Einsteinian problem,
the electron was affected by the field in which additional fields could arise and
disappear. Here we consider a constant lumped force, and in translation from one IRF to
another, also inertial frame, additional fields would be absurd, they just would violate
the conservation laws, true? Second, the moving frame in case of electron was
quasi-inertial only in a small interval of time. In our case the inertia of resting and
moving frames is not limited in time, therefore we can follow the pattern of body’s
trajectory in a considerable time interval, doing not exceeding the limits of model. And
third, Einstein premised from the beginning that the Newton second law is true in the
moving frame, and proceeded from it. We do not dare to premise beforehand that the laws of
classical physics are true in relativistic translations. To avoid the necessity to
transform the Newton law with Lorentz transforms, presenting the force vector as the speed
vector, we can make use of the circumstance that, as relativists admit, the resting frame
of classical mechanics is identical to that in relativity: “Relativistic
mechanics proceeds from the premise that in the coordinate system K’, in which
the material point rests at the considered moment, the laws of motion of old mechanics are
true” [W. Pauli. The theory of relativity, p. 170]. We can add, according to
the above cited Einstein’s statement of problem, Einstein thought the Newton law true
also in the frame relative to which the material point (in that case electron) moves; so
on the grounds of Newton second law we can immediately write the body’s trajectory
and then transform the trajectory, not forces, in premise that there is no difference,
whether we observe the accelerated motion of body in the moving IRF by the measures and
clocks related to it or we observe the uniformly moving body. Basing on this technique, we
get the possibility to compare the body’s motion in the resting and moving frames,
doing not premising beforehand, which is the law of body’s acceleration in the moving
frame under affection of force, and we can analyse, whether the basic law of dynamics is
true and the patterns of trajectories of motion are comparable. If the pattern of
variation of speed and acceleration in frame-to-frame translation conserves, the pattern
of force’s affection is conserved, too. If the pattern of variation of speed and
acceleration in frame-to-frame translation does not conserve, this will naturally mean
that the pattern of force’s affection changes. To reveal it clearer, we will not
premise that in the resting frame the mass of body changes with speed.
Thus, with account of premature conditions, suppose, in
some resting (unprimed) frame, the body A having mass m moves with the
constant acceleration a along the axis x. From a definite arbitrariness of
choice of resting frame, suppose that at the initial moment of time t0
= 0 the body was at the coordinate origin, i.e. x0
= y0 = z0 = 0, and the speed of body at this moment is zero, too,
i.e. u0 = 0. As the body moves along x, we can further
disregard the coordinates y and z, they will not vary.
Proceeding from the statement of problem, the body’s
trajectory will be |
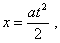 |
(d1.12) |
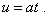 |
(d1.13) |
To be able to study the pattern of body’s motion in
the moving frame, suppose, this (primed) frame moves respective to the resting frame with
some constant speed v with +x , at the initial moment of time the coordinate
origins of both frames coincide and t'0 = t0 = 0, which is in a full agreement with the initial
conditions usually used by Einstein to simplify the computations..
We will translate from the unprimed frame to that primed
through the trivial Lorentz transforms |
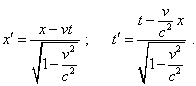 |
(d1.14) |
Substituting (d1.12) into (d1.14), yield |
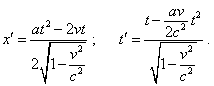 |
(d1.15) |
In the yielded equations (d1.15) the parameters of primed
frame depend on the same parameter of time in unprimed frame. And if we eliminate this
last parameter of resting frame, we will yield one equation describing the motion of body A
in the physical time of moving frame. As we are interested in the trivial appearance of
regularity for coordinates in time, let us represent the second equation of (d1.15) as |
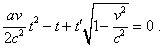 |
(d1.16) |
The solution of this quadratic equation is |
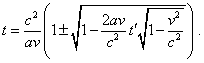 |
(d1.17) |
The equation (d1.17) to provide the equality t'0
= t0 = 0 at the initial moment, choose minus before the root,
so the solution will take the appearance |
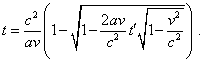 |
(d1.18) |
Now, substituting (d1.18) to the first equation of
(d1.15), yield |
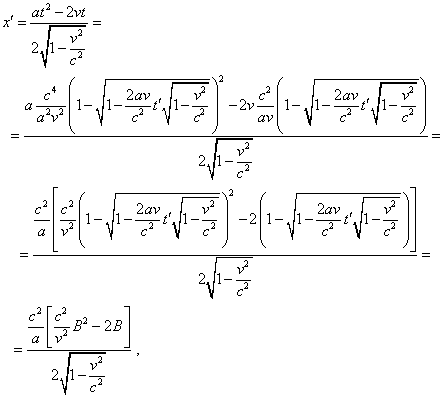 |
(d1.19) |
The yielded expression (d1.19) describes the sought
pattern of motion of the studied body in the moving frame from the view of Relativity.
From the solution we immediately see that time during which the body can accelerate is
limited from the point of moving frame; it is determined by the interval in which the
value B remains constant, while according to (d1.12), the body can move in the
resting frame unlimited time. We could speak here of impossibility to move with the speeds
exceeding the lightspeed, but then the coordinate of body would not become imaginary, it
would remain some constant speed when reached the lightspeed. While here we deal with a
clearly illogical transformation which the Lorentz transform suggests.
VLADIMIR: As I see, the expression (d1.19) can be
effectively simplified. Opening brackets, yield |
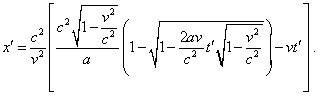 |
(d1.20) |
SERGEY: I agree, and this is important for further
operation with the yielded solution. We are interested in the law of body’s
acceleration from the point of moving frame. The second derivative of coordinate in time
in (d1.20) is |
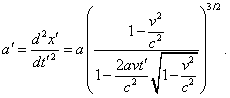 |
(d1.21) |
The graph plotted with (d1.20) is shown in Fig. 3. |
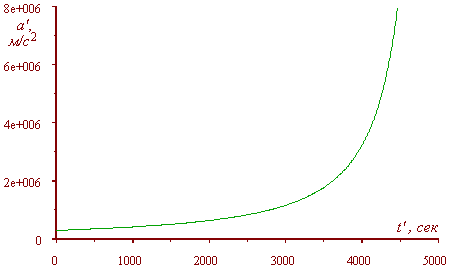
Fig. 3. The body’s acceleration against time in the
moving frame with the speed of moving frame v = 0,1 c, m/s,
and constant acceleration of body in the resting frame a = 0,001 c, m/s2
|
And what is your impression of this regularity, dear
Vladimir?
VLADIMIR: Before I answer, can I, dear Sergey, tell my
impression of the problem you showed? Accelerations are surely very painful point of
Relativity, real ‘nail in a shoe’, and quite large nail. Of course, they pretend
that there is no ‘nail’. For example, their ‘Talmud’ – L.D.
Landau and Ye.M. Lifshiz, vol. 2, “Field theory” – mentions acceleration in
passing, in few lines in the end of section 7 which whole is less than a page; this means,
accelerations are such trifle that nothing to say about, nothing unclear with them. And
then they give the problems on ‘relativistic uniformly accelerated motion’. What
follows from it? First, that they think c invariant in all cases. Without any
proof. So to say, ‘the wife of Caezar is above any suspicion’.  . .
SERGEY: I would say, dear Vladimir, that basically, the
uniformly accelerated motion is not such in Relativity. In the book you mentioned,
acceleration is taken constant relative to its actual frame: “Relativistically invariant condition of uniform
acceleration has to be represented as the constancy of 4-scalar which coincides with w2 (where w is the 4-acceleration – Sergey) in its own (! – Sergey) reference frame: |
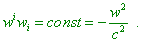 |
(d1.22) |
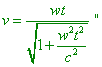 |
(d1.23) |
[ L.D. Landau and Ye.M. Lifshiz, vol. 2, Field theory, p.
39]. As you can see, in relativistic calculations also, with all that they think the
acceleration already not a vector but a scalar and they don’t solve the problem
straight, as they do it with uniform speeds (though, I already said, nothing differs the
technique to observe the accelerated motion from that to observe uniform motion), and they
use the pseudo-accelerated frame through the permanently changed inertial frames, having
not substantiated the validity of such use, – with all that, relativists yield
non-uniformly-accelerated motion in the stationary frame.
And this is not the feature of Landau’s
representation. For example, W. Pauli gives same definition of uniformly accelerated
motion: “As the uniformly accelerated motion in relativistic
kinematics (! – Sergey) we may naturally (?! – Sergey) think such
motion for which the acceleration has permanently same value b
in the frame K' accompanying the body at the moment (! – Sergey) or the material point. The frame K' for each moment of time is
other; in one definite Galilean frame K the acceleration of such motion is
inconstant in time (just what you and me yielded in calculation – Sergey). Such are things with rectilinear uniformly accelerated
motion” [W. Pauli. The theory of relativity, p. 114].
Furthermore, for this acceleration, the 4-interval also is
changed in Relativity. In case of uniformly accelerated motion in the resting frame, it
has already other appearance: “A
special interest there have the formulas for translation of acceleration from the frame K'
that accompanies the body at the moment to the frame K relative to which the body
moves with the speed u. If we direct the axis x with the speed, we will
yield for this case… From (194) we easily yield through integration: |
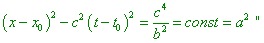 |
(d1.24) |
[W. Pauli. The theory of relativity, p. 113–114].
With it, the very fact that the 4-interval changes in case
of accelerated motion evidences, relativists might not expand the regularities of
uniformly accelerated motion onto the accelerated on the whole and the more use them,
translating into so-called actual frames, if on the whole, even in non-accelerated frames,
their 4-interval does not remain in its initial appearance. We see from (d1.24) that at b
= 0, i.e. in absence of acceleration in our understanding, the right part of (d1.24) does
not become equal to c2 , neither to ds2, but turns into
infinity. This means, in Relativity, the condition b = c corresponds to the
absence of acceleration, which is nonsense, as, I can repeat, according to Relativity, we
have to think the uniformly accelerated motion “such motion for which the acceleration has permanently same value b in
the frame K' accompanying the body … at the moment”.
As you see, here they also play on the
‘obviousness’ of classical concepts. When any physicist is said of uniformly
accelerated motion, he understands this term in the exact meaning and interrelates it with
the stationary (lab) frame, not with the frame accompanying to the accelerated body at the
moment.
VLADIMIR: Indeed, for kinematic theory that describes
translations between IRFs (!), the translation to the accelerated ‘accompanying
frame’ is a prohibited operation. I understand so: it is something like
‘retroactive law’ or, as the humorist said, ‘seven write, three keep in
mind’. These are some tentacles of GRT seen from the spine of SRT. But however they
present it, it seems ridiculous. Only the formula (d1.24) looks really strange, as the
negative left part is equalised to the positive right part. Is it possible, Pauli has
mistaken?
SERGEY: This is shrouded in mystery, dear Vladimir. See
yourself, the system of equations (194) to which Pauli refers in the citation is |
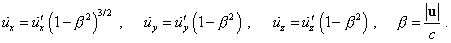 |
(d1.25) |
In its turn, this equation Pauli yielded, joining two
systems of equations for each frame (Pauli’s p. 113): |
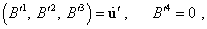 |
(d1.26) |
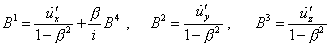 |
(d1.27) |
and the equation of interrelation |
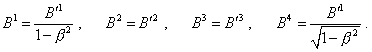 |
(d1.28) |
The substitution of (d1.26) and (d1.27) into (d1.28)
basically has to give the following expression for the first expression of the system
(d1.25): |
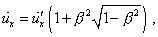 |
(d1.29) |
not to the expression which Pauli wrote. But even if the
first expression of Pauli’s (d1.25) is true, – and Pauli says, “these relationships ((d1.25) – Sergey) are already in the first work by Einstein” (I can mention, I
did not find it in the first either few first works by Einstein – Sergey) [W. Pauli.
The theory of relativity, p. 114]. Then, given the statement of problem |
the prototypal curve has to be found from the expression |
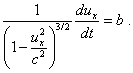 |
(d1.30) |
Perhaps you will agree, it is not so simple to find the
prototype of the left part of (d1.30), and we have to find the second interval, which will
be more difficult. So I approach this matter very simply: several generations of
relativists have been educated on this book, and we still heard no claims. The more that
according to Born, the left part of (d1.24) is not negative: “We can call |
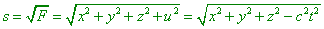 |
(d1.31) |
‘the 4-D distance’, but we have
to bear in mind, we use this expression only symbolically. Proceeding from our invariant F,
we can easily interpret the real meaning of the value s. Let us confine ourselves
to the plane xt (or xu); then |
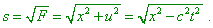 |
(d1.32) |
Further, for any space-like world line, F
is positive, which means, s as the square root of positive number is a real value.
Then we can make the world point (event) x, t simultaneous with the origin,
by way of proper choice of the frame S. At t = 0 we have s = (x2)1/2 = x as the spatial distance from the world point to the
origin” [M. Born. The Einsteinian theory
of relativity, p. 298–299]. Note, both in (d1.31) and in (d1.32) the 4-interval has
been written as in Pauli’s (d1.24). Though you are right, of course, for the
trajectory of material body the difference in the left part of this expression has to be
negative at v < c . Such arithmetic, dear Vladimir. So the most reliable
is to analyse the results shown by relativists themselves, and this is enough to show
their approach to the physical problems untrue. |
Title
page: /1 / 2 / 3 / 4 / 5 /
|
|







