PAGE 4

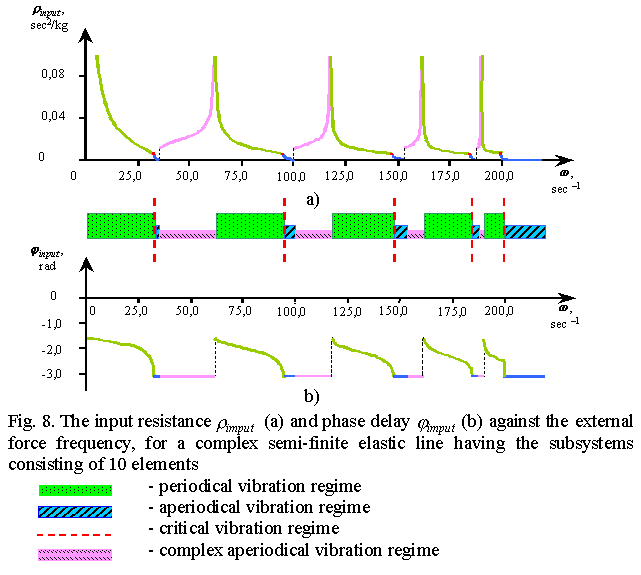
Going further approaching to the real-world models, suppose that each element of an elastic line is in its turn some elastic subsystem having some spectrum of resonance frequencies. The considered method gives here also the answers so necessary for the practice. In Fig. 8 we present the regularity of the input resistance for a semi-finite line having the resonance subsystems as a function of frequency; it is equivalent to the amplitude-frequency characteristic at the line input. We see in it a number of peaks typical for resonance systems described in literature, e.g. in [17], [23], [27] etc. None the less, there is a distinction. The scale of regimes is shown under the plot, and one can see that the aperiodical vibration regime arises first before the first resonance peak, which is absolutely untypical for usual resonance systems, not speaking that these resonance curves have been constructed for a semi-finite elastic line, where after a conventional concept of direct and indirect waves superposition the resonance conditions are absent. Furthermore, the aperiodical regime repeats before each resonance. The resonances in their turn are located at the junctions of the periodical regime and the complex aperiodical regime being new in the vibration theory. And the number of peaks is not equal to the number of subsystem elements - by rough estimation, it is twice less, which also is not typical for resonance systems. It is explained by the fact that a standard vibration process investigated above bifurcates at the critical band in the models having the subsystems, and between the critical frequency for the system as a whole (lower bound) and that for the subsystem (upper bound) the resonance phenomena seen in Fig. 8 arise. Just here may be the reason, why, with the strenght computations ideally done by conventional methods, the ruining happens sometimes in the most unexpected places.

The resonance peaks appearance in elastic systems far from always is conditioned by the presence of specific bounds, heterogeneities or resonance subsystems. It is suffucient to have a kinked line with inequal longitudinal and transversal stiffness coefficients, which is typical for most of construction materials. As an example consider one such lumped system.

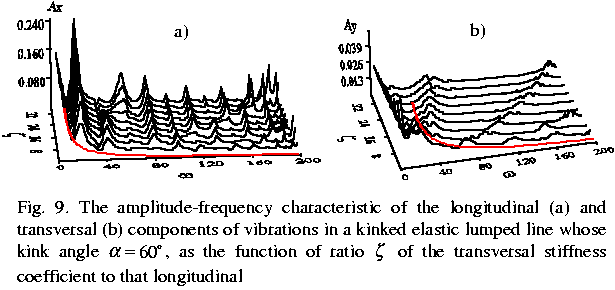
In Fig. 9 we show the amplitude-frequency characteristic of vibrations in a kinked elastic line. On its start there acts an inclined harmonic force depending on the ratio of the transversal stiffness coefficien to that longitudinal. It is seen that at =1 (the near curve) neither longitudinal nor transversal component has the resonance peaks. With growing the resonance peaks arise by quite complicated regularity. Some peaks arise only at large . The amplitude of some peaks first grows and then, with growing , falls but stays finite; some peaks merge or redistribute between the neighbouring peaks, though the solution has been obtained for an ideal line and by all canons in this case all resonance peaks must be infinite. The distance between the peaks in Fig. 9b increases with the growing . The reason is that by the construction condition the growing ratio was caused by the growing transversal stiffness coefficient of the elastic line constraints. Such complex resonance pattern forms dependently not only on but also on the kink angle.

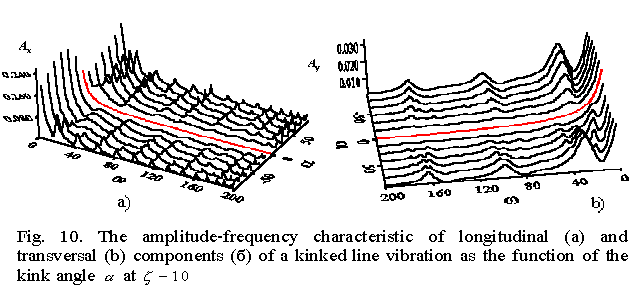In Fig. 10 we show this amplitude-frequency characteristic. One can see from it that in the kink absence (the central curve in red) the resonance peaks disappear even at inequal longitudinal and transversal stiffness coefficients.

Next page