87

Bend effect on vibration pattern

The conventional model of a tectonic earthquake [9, pp.242–244] states that the Earth surface receives the radial push from the depths to 700 km down that comes up to the surface as longitudinal, transverse and Rayleigh waves whose different propagation velocities (9,6; 5 and 3–3,5 km/s respectively) cause three shake phases [10, pp. 290–297], [11], [12]. With it the vertical motions of the crust cause faults, cracks, breaks, and “the earthquakes epicentres are located along the most cracks, or these cracks are the epicentres themselves. In the table-lands the seismic phenomena are much uncommon… However the large crack along the east Madagascar shore seems to be coinciding with the line of often, though weak earthquakes. The same the Ethiopian Fault with its extension along the Red Sea and the Jordan Valley coincides with the earthquakes region including the seismic centres of Lebanon and the Abyssinian plateau. After Toroddsen’s data, the Island seismic regions coincide with those separated one from another by the faults. The Rhine fault depression, between Basel and Mainz, multiply encountered the earthquakes, though negligible… Sometimes the seismic motions propagate along the entire horst, while the adjoining subsided areas stay more or less stable. The longitudinal cracks of ancient mountain ridges sometimes also are the shock lines, as for example the Caledonian channel cracks in Scotland. And the cracks related to the bends of wreath-likely placed folded mountains are especially liable to the earthquakes, and this coincidence is specifically inherent in tertiary mountain ranges surrounding Asia. More often than elsewhere on the Earth the seismic motions reveal in the Japan Great Graben. Almost all Indian earthquakes are concentrated in the corners where the Himalayan Arc meets that Iranian from one side and Malay from another. Unfortunately, sufficient attention still was not given to the close dependence of the folds meeting lines with the shock lines. But this dependence is observed in the ancient folded areas; for example the epicentre of Scandinavian earthquake 23 October 1904 was located on the axis of Christiania depression, and the swarms of Foggland earthquakes were concentrated in the corner formed by the Ore mountains and Thuringian forest” [10, pp.301–303].

The earthquakes caused by the tangential motions of crust being most often and intensive [10, p. 303] “are concentrated almost exceptionally in the mountain ridges that formed not so long ago… thus, almost all seismic zones… are located in the geosynclines in which they are inherent” [10, p.303]. Furthermore, “the degree of shores seismoability corresponds to the degree of steepness of their slopes” [10, p.304].

The problems of such type are usually solved as the solid body vibration problems [13], [14], [15], [16], [17]. However on the whole it is much more complex mathematical problem to take into account all features. For example, according to [18], “the solid rocks in non-disturbed state occur very seldom… Long time the builders did not pay due attention to this circumstance or even omitted it at all. Even now one can often hear the incorrect opinion that the solid rock is some integral, continued ‘whole body’… Such concept is corroborated almost nowhere in nature and is basically wrong. In the view of mechanics, the rock-mass is the ‘many-body system’ ([18]) ‘similar to a dry masonry of well-adjusted stones’ ([19])… With a complete natural partition…, when the rock-mass is ‘run trough by cracks’, and the separate bodies limited by the cracks are perfectly isolated, like the building stones in a container or in mosaic, the rock can be properly named a many-body system… If a monolith was considered a continuous medium and obeyed the continuum mechanics regularities, then the few-body and many-body systems (middle-cracked and strong-cracked systems) are discontinuous, discrete mediums whose behaviour has to be determined by the regularities of discontinuous mechanics, the science not existing yet” [18, pp.14 – 15].

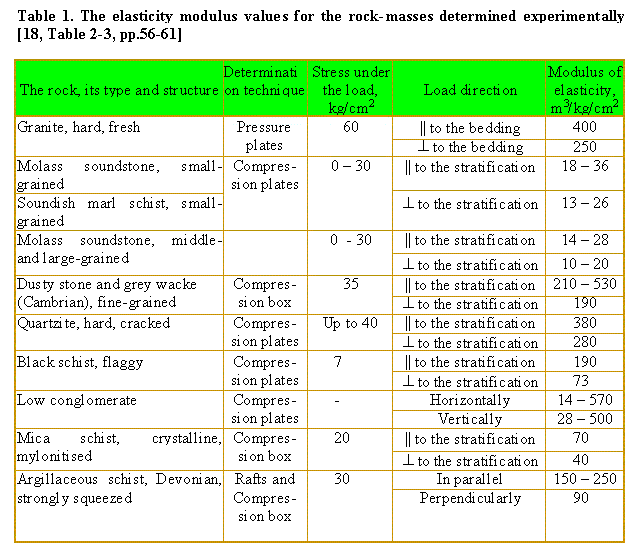
Furthermore, when modelling the processes, the inequality of longitudinal and transverse stiffnesses of an elastic system is the matter of great importance. The Table 1 taken from [18, pp. 56–61] shows that for the main rocks a ratio of transverse elasticity modulus to that longitudinal is approximately 1 to 1,5–2. The more, we have to mark a well-known experimental fact that “one and the same material is able to behave elastically, plastically, viscously or brittlely, dependently on the nature, value and time of the load acting… If we, being guided by methodical considerations, admit (in our mind or experimentally) that these factors are constant, then we can mathematically describe the separate types of material behaviour; with it we speak about the properties of material as of its constants, though in reality they on the whole and each separately are variable” [18, p.46]. "For many materials the modulus of elasticity E has been determined dependently on time and speed of loading… The slowly applied and long-lasting load diminishes, and the fast and short-term load increases the value of elasticity modulus E ” [18, p.51].

Proceeding from the said, we can describe quite completely many salient features of a vibration pattern in so complicated mechanical systems, investigating 1D lumped models having a bend at some kth element and introducing different longitudinal and transverse stiffnesses of elastic constraints. It became possible with the newly discovered method to obtain exact analytical solutions for 1D systems having unlimited number of elastically connected bodies that gives basically other approach to the problem. The new method presented in [20]–[24] considers the elastic system not as an aggregate of vibrant elements, as conventional methods do, but describes analytically the response to the external action of the elastic line as an integral lumped system. This method works equally successfully for finite and infinite, ideal and resistant, homogeneous and heterogeneous elastic systems.

The full complex of problems contoured above is very wide, complicated and diversiform and cannot be described in the frames of one paper. So we will concentrate our attention on the influence of a bend in an elastic line on the pattern of vibration process, supposing that when continued, this investigation offers to describe additionally a broad complex of phenomena being out of frames of this paper.

Having now exact analytical solutions for elastic lumped and distributed systems [20]–[24] obtained without any matrix methods and fully determined in reference to the parameters of studied elastic systems, we gain the possibility to find exact analytical solutions also for the lines having one or more bends. The proof of theorem much simplifies our task to find solutions and the analysis of vibration pattern for a wide class of elastic systems. In this paper we will consider some of the most typical examples that can be investigated in frames of validity of the theorem.