| V.2 No 1 | 95 |
| Bend effect on vibration pattern | |
|
|
| 5. 1 D homogeneous elastic line having inequal longitudinal and
transverse stiffness coefficients
As we said in the introduction, the rocks with which we deal in geological and engineering problems are usually differently deformable in the longitudinal and transverse directions of a rock. So as the third example we will consider the vibration pattern variation in case of inequal longitudinal and transverse stiffness coefficients of an elastic line. In the item 2 we proved that in this case we cannot ignore the bend. Two parameters characterise now the constraints stiffness – the longitudinal slt and transverse str stiffness coefficients. The modelling systems of equations for the semi-finite homogeneous elastic line takes the following form: for the longitudinal component |
|
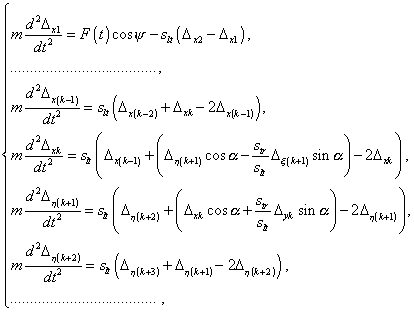 |
(28) |
| and for the transverse component | |
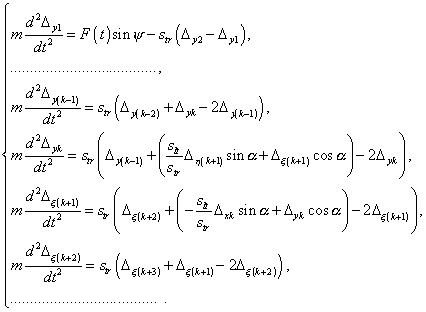 |
(29) |
The systems (28)-(29) differ from
(1)-(4) by the kth and (k + 1)th equations of the modelling systems. The
displacements of transient line elements |
|
| (30) | |
which disables us transforming the
coordinates ( |
|
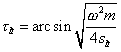 and and 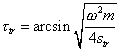 , , |
(31) |
characterising the delay of along-the-line propagation of longitudinal and transverse components of the wave, and in general case these parameters differ. In this connection, the critical frequencies for the longitudinal and transverse components are also different and equal to |
|
| (32) | |
relatively. It causes the division of the frequency range not into two but into tree sections. In that first the vibrations of both longitudinal and transverse components relate to the periodical vibration regime. With the typical relationship of stiffnesses |
|
| (33) | |
this band has the bounds 0
< |
|