V.2 No 1 |
17 |
| Homogeneous 1d resistant line | |
|
|
V.2 No 1 |
17 |
| Homogeneous 1d resistant line | |
|
|
Some features of vibrations in homogeneous 1d resistant elastic lumped line Sergey B. Karavashkin and Olga N. Karavashkina Special Laboratory for Fundamental Elaboration SELF e-mail: selftrans@yandex.ru , selflab@mail.ru
In this paper we will consider, how resistance affects vibration processes in a semi-infinite elastic lumped and distributed lines. We will see that for the given type of line, the progressive pattern of vibrations remains also at the overcritical frequencies, and the phase delay is always less than the value corresponding to the first Brillouin zone. Comparing the obtained results with experimental data of the phase velocity of ultrasonic wave in the carbonic acid gas, we will see that taking the resistance into consideration, we can essentially refine the conventional models and promote their better correspondence to the experimental data. Keywords: many-body theory, wave physics, complex resonance systems, ODE Classification by MSC 2000: 30E25; 70E55; 70J35; 70J60; 70K40; 70F40 Classification by PASC 2001: 02.60.Lj; 05.10.-a; 05.45.-a; 45.30.+s; 46.15.-x; 46.25.Cc; 46.40.-f; 46.40.Fr |
1. Introduction Most of applied models take into account the dissipative force of resistance. Many works, in particular [1]–[9], have been devoted to this subject. But this study is difficult because of few factors. First of all, conventional mathematical methods for elastic lumped lines calculation lead, as a rule, either to the matrix methods that for multibody systems can be solved only numerically, or immediately to the numerical methods like Ritz method, asymptotic methods and some others. For example, in [8], for a conventional modelling system based on Lagrange equation |
| (1) |
(where Qje(t)
are the given functions of time, ajk , bjk , cjk
, |
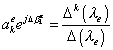 |
(2) |
(here |
Contents: / 17 / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 / 29 / 30 / 31 / 32 / 33 / 34 /