SELF |
26 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
26 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
4. Limit passing to a distributed line The exact analytical solutions (19) yielded for a lumped line can be easily extended to that distributed. To do so, we have to substitute the parameters characterising the discrete mass distribution for a corresponding system of parameters characterising 1D system of distributed masses. Introduce |
| (29) |
where Noting (29), we can determine the transformation of
parameters (16)–(18) at a |
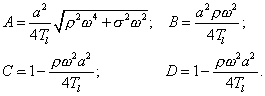 |
(30) |
Substituting (30) into (16), we obtain accurate to a: |
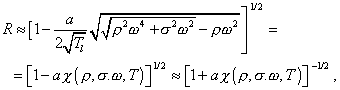 |
(31) |
where the damping coefficien |
contains only the values corresponding to a distributed system. In further studying the parameter R, we have to note its power in (15). Then from (29) and (31) we can write |
| (32) |
It means, when transiting to a distributed line, the
along-line damping is described by an exponential regularity. In transiting to an ideal
line, i.e. at |
Contents: / 17 / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 / 29 / 30 / 31 / 32 / 33 / 34 /