V.5 No 1 |
57 |
| Three-body problem in collision theory | |
|
|
V.5 No 1 |
57 |
| Three-body problem in collision theory | |
|
|
| To 75th anniversary of the Physical-Engineering
Department of Kharkov Polytechnic University (Alma Mater)
EXACT SOLUTION FOR THE PROBLEM OF ELASTIC INTERACTION OF THREE AND MORE POINT MASSES IN THE COLLISION THEORY S. B. Karavashkin and O.N. KaravashkinaSpecial Laboratory for Fundamental Elaboration SELF 187 apt., 38 bldg., Prospect Gagarina, Kharkov, 61140, Ukraine phone +38 (057) 7370624 e-mail: selftrans@yandex.ru , selflab@mail.ru We will put in order the solution for the problem of two bodies in the collision theory and develop this ordered solution for the three-body problem. This development appeared possible when noting that at the moment of n bodies interaction each mass interacts simultaneously both with the rest masses of the considered system and with the local centre of their masses. Due to this, the problem of n bodies can be divided into n two-body problems consisting of the studied body and local centre of masses. Classification by MSC 2000: 70F05; 70F07; 70F10 Classification by PASC 2001: 45.50.-j; 45.50.Jf; 45.50.Tn; 82.20.Fd Keywords: theoretical mechanics, collision theory, three-body problem, n-body problem, trajectory of mass centre of the system of bodies
|
| 1. IntroductionThe problem of two or more bodies has been addressed from
Newton's times. Many prominent scientists of past centuries studied it with different
degree of success: these were Laplace, Caushy, d'Alambert, Varignon, Jacobi, Poincare,
Levi-Civita and many others.
From the very beginning this problem has been separated into two main trends: scattering theory and collision theory that form the general underpinning of interaction theory. Each of these theories in its turn includes the theories of elastic and inelastic interaction. In frames of elastic interaction, the scattering theory
proceeds from the fact that the studied masses interaction is continuous and limited only
by the case "when the forces acting among the particles depend
only on the distance between them |
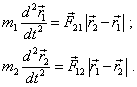 |
(1) |
The exact solution for the two-body system (1) is conventional [2, p. 104- 109]. It is based on the transition to the reference frame of mass centre of two-body system, due to which (1) can be described by one equation |
| (2) |
where |
| (3) |
is the reduced mass of the system of interacting bodies, and |
| (4) |
is the radius-vector describing the mutual motion of bodies. In transition to the system of interacting bodies (n > 2) , the general modelling equation can be recorded as follows: |
| (5) |
The dot in the right part of (3) indicates that we eliminate from the summation the term with j = i. In connection with modelling system that became more
complicated, there come to light some additional difficulties in seeking its solution [3],
[4]. "The efforts of
many famous mathematicians have been devoted to this difficult problem, including Euler and Lagrange (1772), Jacobi (1836), Hill
(1878), Poincare
(1899), Levi-Civita (1905), and Birkhoff (1915). In 1772, Euler first introduced a synodic
(rotating) coordinate system. Jacobi (1836) subsequently discovered an integral of motion
in this coordinate system (which he independently discovered) that is now known as the Jacobi integral.
Hill (1878) used this integral to show that the Earth-Moon distance remains bounded from
above for all time (assuming his model for the Sun-Earth-Moon system is valid), and Brown
(1896) gave the most precise lunar theory of his time" [3]. At the same time, irrespectively of the number of interacting bodies,
(5) always is definite, as the number of unknown radius-vectors |