SELF |
62 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
62 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
To yield the final solution for the studied case of interaction in the mass centre frame on the basis of (31) and (32), we have to account additionally the equality of momenta in the given frame, which follows from (23). Noting (21), we yield with it |
| (33) |
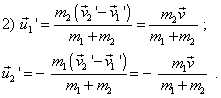 |
(34) |
Comparing (34) with (33), we see that in the mass centre frame, after the collision, the speed vectors simply changed their direction to the opposite, which with the before-proven momenta equality in the given frame fully corresponds to the action and reaction equality law (Newton third law). Thus, in the mass centre frame two variants are possible: either each body retain its speed or only their direction changes to the opposite. This makes considerably easier to yield the final solution of two-body problem in general. It is sufficient now to substitute (33) and (34) in (13): |
| (35) |
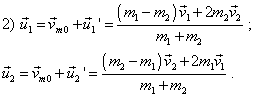 |
(36) |
The expressions (35) and (36) are the sought general solution for 2 D case of mutual motion of the bodies. It is typical that this solution fully coincides with the above solution of 1 D problem (31), (32). The only aspect that we need to note in solving, we have to take into account that bodies must come to the point A simultaneously, as with it in the statement of problem there appear additional limitations in the choose of values of initial locations and speeds of bodies. |
|
Fig. 5. The construction to complement the initial conditions in the two-body problem under condition of both bodies simultaneously coming to the interaction point A
|
For example, giving the point A, we in this way complement two parameters. Actually, the bodies to come from their initial locations B and C to the point A (see Fig. 5), it is necessary they to spend identical time to pass their ways BA and CA. Proceeding from this, it follows from Fig. 5 that the equalities |
| (37) |
and |
| (38) |
have to be true. From (37) and (38) we can complement two initial conditions - for example, fully complement the initial location of one body. Then, giving additionally the time tA in which the bodies will collide, we can with Fig. 5 complement two more parameters. Actually, it follows from Fig. 5 that |
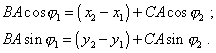 |
(39) |
Since |
| (40) |
then |
| (41) |
As we see, (37), (38) and (41) fully determine, e.g., the initial location of bodies, either all parameters of their speeds, or all initial parameters of one body. Noting (37), (38) and (41), the solving of two-body problem (35)- (36) becomes fully determined, as these expressions determine the conditions of certainly simultaneous arriving of both bodies to A. We also see from this analysis that in case of 3 D interaction of two bodies, the above solutions remain valid, as anyway the two-body interaction will occur in the plane; and the turn of plane as to the basic planes of 3 D basis does not change the solution in the inertial frame. This last will be of importance in the view of further consideration of three and more bodies. |
|
Fig. 6. The point masses trajectories. The construction
parameters: m1 = 5 kg, m2 = 3 kg,
|
To illustrate the solution, in Fig. 6 we show the animation of trajectories of point masses. It is well seen that generally Snellius law (equal angles of falling and reflecting beams) is untrue. Above all, this means that when in studying the particles interaction we encounter some trajectories irrelevant to conventional understanding based on the incomplete solution of two-body problem, before premising some third particles distorting the reflection angles, we have to analyse very attentively the parameters of two interacting particles. |