SELF |
64 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
64 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
At the same time we can form the local mass centres, there will be three centres for the three-body problem. Each will be determined as follows: the first local mass centre |
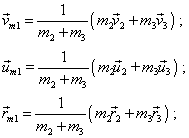 |
(49) |
the second local mass centre |
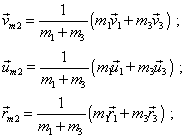 |
(50) |
and the third local mass centre |
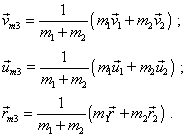 |
(51) |
Undoubtedly, in the three-body system we can write the after-collision conservation expression for no one of these local mass centres, as we did it in (46), since in general case |
| (52) |
At the same time there exists the feature of modelled problem which allows to use the local mass centres to complement the basic system (42)- (43). To corroborate the said, pay attention that all three bodies will collide simultaneously in the frame S, all masses are point and the main, when colliding, all three local mass centres will be located at the same point A. This means, each mass will interact, on one hand, with two rest masses and on the second hand - with the mass centre of these two bodies, which fully describes both the measure of inertia and momentum of the system of bodies composing it. It is important that this feature cannot be separated from the statement of problem: if the local mass centre does not arrive into A to the instant of interaction, this will mean that some of bodies that determine this mass centre location is not at the point of interaction and does not interact with the third body. Because of it, the tree-body problem in fact is divided into two sequential two-body problems which we can solve using the above technique. From this description one more important conclusion follows. Since the mass centre fully identifies two masses composing it, this centre as the unit will interact with the studied third body strongly in accordance with the statement of two-body problem. Consequently, the plane in which any body will interact with the mass centre of two other bodies will go through the initial locations of this body, local mass centre and point A, as shown in Fig. 8. |
|
Fig. 8. The plane of interaction between the mass mi = 1, 2, 3 and local mass centre of two rest interacting bodies |
| With this nuance, the three-body problem is divided into three identical two-body problems; in each one body will interact with the mass centre of two other bodies. It is easy to check that with it we obtain all deficient equations complementing the basic system of equations (42)- (43). Noting this feature of point masses interaction, we can complement the basic systems of equations for any number of masses, solving sequentially the identical two-body problems for the chosen masses of system and local measure of inertia of the centre of rest masses involved into the studied conservative system. |