SELF |
16 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
16 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
|
The method to seek the solution for some types of nonlinear wave equation S. B. Karavashkin and O.N. KaravashkinaSpecial Laboratory for Fundamental Elaboration SELF 187 apt., 38 bldg., Prospect Gagarina, Kharkov, 61140, Ukraine phone +38 (057) 7370624 e-mail: selftrans@yandex.ru , selflab@mail.ru We will show the technique to seek the solution for nonlinear wave equations like u’’ + g(t)u = 0 and u’’ + g(u)u = 0. We also will consider the possibility to broaden the application area of this technique for other types of nonlinear wave equations. Keywords: wave physics, mathematical physics, second-order nonlinear differential equations, wave equation Classification by MSC 2000: 33E15; 35L05; 35L70; 35J15; 35J50; 74J30 Classification by PASC 2001: 03.65.Db; 03.65.Ge; 47.20.Ky 1. Introduction The wave equation is known to be important in modelling of physical provesses in many problems of thermodynamics, mechanics, field theory etc. In many cases of modelling we face nonlinear types of wave equation. In lack of approaches to solve, we have either to linearise the problem without grounds or confine ourselves to the numerical methods of solving, which much limits the possibility to develop the solutions in their applications and disables the full analysis of the model. In this paper we will show the technique to solve nonlinear wquations of two types important for modelling and some ways to extend its application for other types of nonlinear wave equation. 2. The method to find the solution for the wave equation like u’’ + g(t)u = 0 As we already pointed in the caption of this item, consider a wave equation of the type |
| (1) |
to reveal the way to seek, let us first transform the left part. Multiply the second summand by - i2, add and subtract if (t) du/dt, where f (t) is some ancillary function of time differentiable in the interval, and divide the function g (t) into two additive summands |
| (2) |
where k (t) is some ancillary function of time differentiable in the interval. Combining, yield |
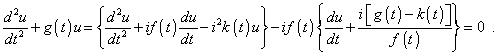 |
(3) |
To find the solution for (3), it is necessary, the expressions in braces to be identical. To achieve it, we can make use of the known expression that follows from the laws of differentiation |
| (4) |
Comparing (4) with the first brace in (3), yield |
| (5) |
from where |
| (6) |
Basing on (4)- (6), we can conclude that expressions in braces in (3) will be identically equal if |
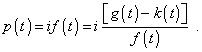 |
(7) |
From (7), noting (6), we have |
| (8) |
or |
| (9) |
The yielded expression (9) determines the unknown function f (t) . Having it found, we yield the solution of general equation (1). We can conveniently seek the solution of differential equation (9) as a harmonic series, like we did it in [1]. For it, we have to represent g (t) also as the harmonic series |
| (10) |
where gm are some constants of the Fourier-expansion, and generally they can be complex values. Noting (10), we will seek the solution for (9) also as the harmonic series |
| (11) |
Having differentiated (11) over the time and substituting the result into (9) jointly with (10) and (11), yield |
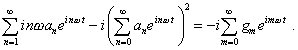 |
(12) |
From (12) we see that the complex unit can be reduced in the right and left parts and with real coefficients gm the equation becomes also real. Further, we can represent (12) as a system of algebraic equations, equalising the coefficients at the related exponentials in the right and left parts. Let us write the first of these equations. m = 0 |
| (13) |
from where |
| (14) |
m = 1 |
| (15) |
from where |
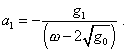 |
(16) |
m = 2 |
| (17) |
from where |
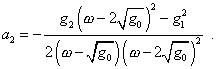 |
(18) |
m = 3 |
| (19) |
from where |
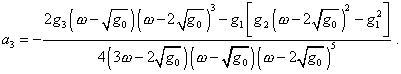 |
(20) |
As it follows from the analysis of four first terms, the
system is recurrent and we may sequentially determine all expansion coefficients through
the previous. From the yielded solutions we also see that the yielded series is fast
decreasing in proportion to 1/ Having determined the type of function f (t) and revealed in this way that the determining expression (9) has a solution, we can return to (3) and write it as |
| (21) |
where |
| (22) |
From (21) and (22) we see that when taking |
| (23) |
we in this way make vanish also (21). This means, the condition (23) is the equation determining one of the particular solutions of (21) and so of the initial equation (1). The solution for (23) is obvious: |
| (24) |
where C1 is some constant determined by the statement of problem. Taking into account additionally the coefficients of the series (11) that we found, we can integrate f (t) over the time and substitute into the left part of (24). We will yield |
| (25) |
To determine the second particular solution of the initial wave equation (1), it is suffucient to rearrange th eterms in (3) and to write it so: |
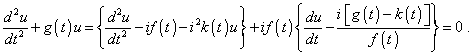 |
(26) |
Now, making the above way, we yield |
| (27) |
where C2 is the constant determined by the statement of problem, too. Joining (25) and (27), yield finally |
| (28) |
This is the sought solution of the wave equation (1). In the particular case |
| (29) |
all expansion coefficients (10), except zero, vanish and the solution (28) takes the trivial appearance |
| (30) |
which corroborates the correctness of our transformations. |