V.6 No 1 |
17 |
| The method to seek the solution for some types of nonlinear wave equation | |
|
|
V.6 No 1 |
17 |
| The method to seek the solution for some types of nonlinear wave equation | |
|
|
3. The technique to find the solution for the wave equation like u’’ + g(u)u = 0 Now, using the technique that we worked out in the first problem, find the solution for the differential wave equation for the case when the coefficient g depends on u , i.e. |
| (31) |
In this expression we intentionally did not represent the second summand of the left part as g1(u)u, as, when introducing |
| (32) |
we in this way come to the general form (31). To find the solution for the equation (32), we need not divide g (u) into two additive terms, as this function does not directly depend on the time parameter. It is sufficient, like in previous problem, to introduce the squared complex unity, as well as to add and subtract the first derivative of some function f (u) smooth in the interval. Yield |
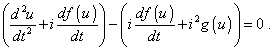 |
(33) |
We can take as this derivative of f (u) introduced in (33) in the second left bracket as |
| (34) |
Substituting (34) into (33), we come to the following expression: |
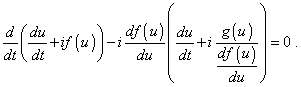 |
(35) |
We see from (35), the expressions in brackets to be identical, it is necessaru and sufficient, the equality |
| (36) |
Integrating (36), yield |
| (37) |
The solution of the equation (36) enables us to find the first particular solution of the main equation (31), because, as we substantiated this technique in previous problem, it is sufficient, the equality |
| (38) |
to be satisfied, or |
| (39) |
which, with the dependence g (u) given in the statement of problem, is already integrable. In particular, in passing to the linear case, when |
we come to the differential equation |
| (40) |
with the trivial solution |
| (41) |
The same as in previous problem, to find the second particular solurion, we have to rearrange (35) so: |
 |
(42) |
With it, the ancillary differential equation for f (u) will be the same, but (38) will be changed and will take the appearance |
| (43) |
or |
| (44) |
The sum of solutions of the equations (39) and (44) gives us the general solution of differential equation (31). In linear case the solution will take its due form |
| (45) |
But this does not mean that in general case the solution of (39) and (44) will be trivial harmonic functions. For example, when |
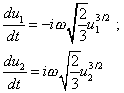 |
(46) |
the solution of this system will be the following expression: |
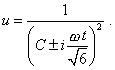 |
(47) |
Basically, we not always can reduce (47) to some exponential complex function. In particular, with the initial condition C = 0 |
| (48) |
4. The scope to develop the technique We showed on two typical kinds of nonlinear wave equation, how to apply this technique. The search of solutions shows, this transformation technique allows to reduce the second-order differential equation to the first-order equation. This much simplifies the search of solution even in case when we have to apply the numerical methods to integrate, not to say that in many cases it gives the possibility to yield the analytical solution, which was impossible before. And these are not all advantages of this technique. It can be successfully appled to quite large class of problems like those considered. In particular, if in the first of above problems, we involve to the equation, above the second derivative and a free term, the first derivative like q (t) du/dt that usually determines dissipative processes in physical problems, we can find the solution with such rearrangement of the terms of the initial differential equation: |
 |
(49) |
The same, if in the second above problem the first derivative like q (u) du/dt is present, we have to seek the solution with the following arrangement of the terms of initial equation: |
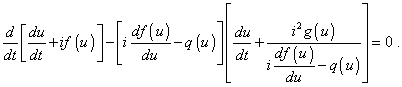 |
(50) |
this last equation gives us the differential equation of the first order |
| (51) |
whose solution determines in fact the way to find the general solution of the problem. |
Reference: 1. Karavashkin, S.B. and Karavashkina, O.N. Investigation of elastic constraint non-linearity. IJMEE, 33 (2005), 2, 116- 133. |