|
SELF |
4 |
| On conservation of energy and impulse |

|
VLADIMIR: Going on carping, I would say, I also don’t
understand exhaustively your consideration after (d1.24). In particular, why the right
part has to be equal to ?2? Usually relativists write s2.
But the fact that the interval turns into infinity at b tending to zero relativists
would have to explain to the folks.
SERGEY: I agree, but I took one of trivial variants. See,
if I take, for example, b = kc, k > 1 and dimensional, it will
happen even worse, as the acceleration, additionally, will be numerically more than the
lightspeed  . So relativists would have to explain not only, why
the right part of (d1.24) turns to zero
with uniform motion but also so large accelerations when uniform motion. . So relativists would have to explain not only, why
the right part of (d1.24) turns to zero
with uniform motion but also so large accelerations when uniform motion.
VLADIMIR: Second, the acceleration, from their view, has
‘to be adjusted’ to the situation in time, so that the speed of material body
could not exceed c, i.e., they mean the acceleration not absolute, as classical
physics does. In classical physics it is the master of situation, while in Relativity it
is the servant of postulate of constant lightspeed. For example, in the relativistic limit
their ‘acceleration’ will be in inverse proportion to the current moment of time
in the resting frame.
SERGEY: Moreover, even if the body reaches the speed of
light in the resting frame, in the actual frame its acceleration will remain, and will
remain the same constant value, which is nonsense as such.
VLADIMIR: I understand what you would like to say, but I
would mention, after relativistic opinion, the body never can reach the lightspeed. So,
from their view, the body can be accelerated infinitely.
SERGEY: On one hand, I agree. And Pauli writes the same: “The speed does not grow unlimitedly but asymptotically approaches
the lightspeed. The related world line is a hyperbola, due to which the uniformly
accelerated motion in relativistic mechanics is called also hyperbolic, as opposite to the
‘parabolic motion’ of old mechanics” [W. Pauli. The theory of
relativity, p. 114]. But let us look on this matter from other side. If we, following the
Relativity in our problem in which we premise the translation between IRFs, establish the
constant acceleration in the moving frame, then in the resting frame we will also yield
the hyperbolic acceleration of body’s motion. Actually, at a' = b = const
and from (d1.18) |
basing on (d1.21),
we yield |
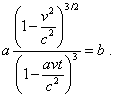 |
(d1.33) |
The plot of this regularity you can see in Fig. 4.
|
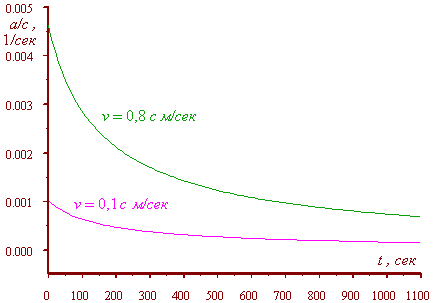
Fig. 4. The body’s acceleration against time in the
resting frame with constant acceleration of the body in the moving frame at different
speeds of moving frame and quantity of constant acceleration of the body in the moving
frame b = 0,001c, ?/???2 |
This graph shows the same hyperbolic regularity that
already is not limited by the condition when the body’s trajectory passes to the
complex plane, and this motion can last infinitely, approaching the body’s speed to
the lightspeed.
But let us ponder on a simple question. We have two IRFs
whose observers watch the uneven motion of a body. In one frame the acceleration is seen
constant, in another hyperbolic. Is not it a direct answer to our question of
non-equivalence of IRFs in Relativity?
VLADIMIR: But in Relativity not (d1.13) but (d1.23) works. And formulas like (d1.11) and (d1.13) they call ‘the law-speed limit’ or
something like this.
SERGEY: Agree, at least that relativists try to present
their formulas in this way. But let us look at the numerator of (d1.23). We see there the
product of some constant acceleration by time, and relativists write it not in the
accelerated frame. In this frame the acceleration would be zero, true? This constant
acceleration is written for the frame accompanying at the moment, it is really an inertial
frame, but for a body, this IRF is new at each moment. But if at each new moment this
frame is already new, relativists already may not find first, the more second
differentials of displacement, within one frame. They have to translate coordinates and
time from the new frame to that previous, and for the second differentials they have to
use translation from two sequential frames. You see, with it nothing to say of constancy
of acceleration in the actual frame, there will be total mess. None the less, relativists
admit, in the IRF whose speed at some moment of time is same as the speed of body, it is
the uniformly accelerated motion. Consequently, at the second and third moment of time
this acceleration is observed from the same IRF. Only in this case we may speak of
body’s acceleration relative to the particular frame. And if at these three moments
of time we saw the body’s acceleration in one frame, we can state that we have
detected the uniform acceleration of the body in the same IRF. Really, let the actual
frame remains same during two intervals of time dt'1
= dt'2 (three specific moments of time), and during these two
intervals of time the body has sequentially shifted by the distances dl'1
and dl'2 . If we have these data, we can find the acceleration b
in this accompanying frame, true? And without these differentials Pauli, as well as all
other relativists, might not write 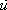 'x , 'x , 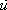 'y , 'y , 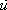 'z in (d1.27), true? But however little were the
increments of time and coordinates of body’s displacement in this actual IRF, we
always can take less and less infinitesimal increments, writing 'z in (d1.27), true? But however little were the
increments of time and coordinates of body’s displacement in this actual IRF, we
always can take less and less infinitesimal increments, writing 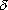 t'1
= dt'1/n and t'1
= dt'1/n and 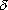 t'2 = dt'2/n, and with these increments find the body’s
acceleration which will be b, too. This means, within the common infinitesimal
increment of time, we can n times measure the body’s acceleration in this
frame and show it constant in this frame, before we take a new actual frame. And if this
constancy remains during an infinitesimal interval of time without transformation which,
relativists say, causes the hyperbolic pattern of acceleration, we can state: as long as
the body remains the law of its motion in this particular IRF (which was at the moment the
actual frame of the body), the body’s motion remains uniformly accelerated, which
means, at least in this frame the classical formula will remain. Proceeding from
equivalence of all frames, this formula will remain also for all other frames. So we see
that in the IRF the classical expression for uniformly accelerated motion will remain. All
the rest only perverts the mathematical formalism for relativistic wishes. t'2 = dt'2/n, and with these increments find the body’s
acceleration which will be b, too. This means, within the common infinitesimal
increment of time, we can n times measure the body’s acceleration in this
frame and show it constant in this frame, before we take a new actual frame. And if this
constancy remains during an infinitesimal interval of time without transformation which,
relativists say, causes the hyperbolic pattern of acceleration, we can state: as long as
the body remains the law of its motion in this particular IRF (which was at the moment the
actual frame of the body), the body’s motion remains uniformly accelerated, which
means, at least in this frame the classical formula will remain. Proceeding from
equivalence of all frames, this formula will remain also for all other frames. So we see
that in the IRF the classical expression for uniformly accelerated motion will remain. All
the rest only perverts the mathematical formalism for relativistic wishes.
Speaking of these discrepancies, I would like to draw your
attention again to Fig. 4. You see in it how the acceleration in a resting frame changes
at two values of speed of moving frame, given the acceleration in each frame is constant.
But does not the acceleration in the resting frame mean that we measure just in this
frame, not via other frames? Well, if so, then according to Relativity it appears that
dependently on, which auxiliary virtual frame we take, such value of acceleration we will
measure in the resting frame. As there is an infinite number of such virtual frames,
including those moving with the sub-light speed, we appear unable to measure even a little
acceleration, taking a frame moving with a sub-light speed as that virtual. Nonsense,
absurd that follows from Relativity’s disability to describe the accelerated motions,
due to which relativists have to measure and to give accelerations not immediately in some
frame but via some intermediate frame relative to which they also cannot satisfy the
conditions of their formalism with rigour required in mathematics.
VLADIMIR: None the less, I think, in this case the
‘admittance’ of relativists that the resting frame of classical mechanics is
identical to the resting frame of relativistic mechanics – “Relativistic
mechanics proceeds from supposition that in the coordinate system K’ in which
the material point at the considered moment rests, the equations of motion of old
mechanics are true” [W. Pauli. The theory of relativity, p. 170], – does
not matter, because it has been done perhaps without enough thought. Most relativists
probably don’t think so. For example, (d1.13) says of unlimited growth of speed,
which is unacceptable for Relativity.
SERGEY: There is nothing new that relativists use to
violate the conditions and limits of applicability of both their and borrowed formalism.
But all formulas related to the acceleration and relativistic dynamics have been built on
the principles and limitations which the founders of Relativity had to establish, seeing
no possibility to agree the solutions with phenomenology in more general way, and all
limitations in case of accelerated motion are reduced to little speeds, to have a
possibility at least approximately to make an appearance as if it is obvious – to use
the formalism of classical mechanics in relativistic kinematics. Should Einstein did not
this limitation, he would have to repeat the work of many, many generations of scientists
who developed dynamics, and in absence of experimental basis which would give him the
grounds to introduce such or other relationship between the affecting force, body’s
mass and acceleration. Not in vain all postulates of Relativity are substantiated so:
‘they are obvious from the view of classical physics and Maxwell theory’.
VLADIMIR: Your claim that in the resting frame,
relativistic kinematics is taken identical to classical is absolutely true. But the
classical physics says, dynamics is far from being kinematics, and it is groundless to
extend here the ‘identity’ with (d1.12),
even if relativists sometimes confuse dynamics and kinematics. Think, dear Sergey, maybe
there is a sense to remain just in the low-speed region, to avoid such great contradiction
to the formalism of SRT. The main regularities of figures will remain, I think.
SERGEY: The regularities of figures are not the matter,
dear Vladimir, so I said before considering the problem, we have to be careful of
indefiniteness connected with relativistic formalisation of the accelerated frame. While
in our example, which we considered with you, factually only the trajectory is described
from the point of two IRFs and relativists reduce the laws of kinematics in one frame to
classical mechanics. Since, as I already showed you, having not given the laws at least in
one frame, relativists are unable to write them in another frame, so the second point is
only outwardly difficult. And they have to write namely in the form in which classical
mechanics does it. Notice, describing the accelerated motion, relativists confine
themselves to the relationship between the actual and resting frames. But we can observe
the same accelerated motion from two inertial frames, cannot we? This situation happens in
modelling more often. Relativists do not answer this question, because this translation is
impossible with their actual frame. See yourself. Such relationship can form exceptionally
through the actual frame that just gives the relativistic hyperbolic pattern of
body’s motion. Above I have written this relationship between the 3-D accelerations
of resting and actual frames (d1.25). Each expression includes the parameter 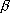 whose value
depends on the momentary speed of the body related to the variation of speed of the
sequence of actual frames. This means, in time, this parameter as such reflects the
accelerated motion of the body. If the resting IRF is one, Pauli says, he had not much
difficulty with the dependence of whose value
depends on the momentary speed of the body related to the variation of speed of the
sequence of actual frames. This means, in time, this parameter as such reflects the
accelerated motion of the body. If the resting IRF is one, Pauli says, he had not much
difficulty with the dependence of 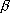 on time, though he had to account the functional type of
this parameter when found the prototypal curve. But if we have two IRFs moving with
different speeds relative to each other and from them observe the accelerated motion of
the body, then, to pass from one frame to another, we have to translate one value of
time-dependent parameter on time, though he had to account the functional type of
this parameter when found the prototypal curve. But if we have two IRFs moving with
different speeds relative to each other and from them observe the accelerated motion of
the body, then, to pass from one frame to another, we have to translate one value of
time-dependent parameter 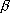 into another. I think, not only we don’t know such
way, relativists also cannot prompt a proper way, as it does not exist, because this
parameter varies in time. And trivial way to sum the speeds is inapplicable, as the
parallelogram law does not work in Relativity even for constant speeds, nothing to say of
summing the inertial and uniformly accelerated motions. Judge yourself. You observe this
hyperbolic motion from the resting frame but would like to calculate not with the direct
formula but with the expression yielded with some virtual frame which you introduced
arbitrarily. As you well know, in classical formalism it will not cause problems. While
here, as we showed in the subsection 7.1.5 of our work, dependently on the chosen speed of
this virtual frame, you can yield any value of the studied speed, even faster-than-light.
And if only direct measurements are true, due to ambiguity of speeds summing in
relativistic kinematics, then it is illegal to interrelate IRFs in observing accelerated
motion, just because the formula for speeds summing is untrue. into another. I think, not only we don’t know such
way, relativists also cannot prompt a proper way, as it does not exist, because this
parameter varies in time. And trivial way to sum the speeds is inapplicable, as the
parallelogram law does not work in Relativity even for constant speeds, nothing to say of
summing the inertial and uniformly accelerated motions. Judge yourself. You observe this
hyperbolic motion from the resting frame but would like to calculate not with the direct
formula but with the expression yielded with some virtual frame which you introduced
arbitrarily. As you well know, in classical formalism it will not cause problems. While
here, as we showed in the subsection 7.1.5 of our work, dependently on the chosen speed of
this virtual frame, you can yield any value of the studied speed, even faster-than-light.
And if only direct measurements are true, due to ambiguity of speeds summing in
relativistic kinematics, then it is illegal to interrelate IRFs in observing accelerated
motion, just because the formula for speeds summing is untrue.
So, solving the problem through direct observation of
body’s trajectories from two frames and giving the trajectory of one IRF, we, you and
me, have avoided many difficulties of relativistic mechanics, and our consideration, as
opposite to the relativistic way to solve, is not limited by v << c ,
because of applicability of Lorentz transforms up to the lightspeed. And we had a full
right to study point by point any trajectories, in that number the trajectory that
describes the uniformly accelerated motion. The fact that relativists use classical
formulas to find the acceleration in inertial actual frames allows us to use these
formulas in inertial frames. Yes, with it Relativity encounters difficulties – well,
when accelerated motion, Relativity is short anyway.
VLADIMIR: To tell the truth, it took much my time to catch
that you consider only the law-speed range (v << c).
SERGEY: As I showed you, I had to go a slightly seen path
between discrepancies within Relativity.
VLADIMIR: I don’t know, how much correct is it –
to take the coordinate transform in their exact form, and the expression for acceleration
– in the limit. So when you wrote “substituting (d1.12) into (d1.14)”,
I long time thought that you are doing ‘a mortal sin’, but then I decided:
nothing terrible, I will see what you yield of it.
SERGEY: There was no sin, of course. See, should in
(d1.12) there was the equation of uniform motion, neither you nor relativists would see a
mortal sin in it, the more that the law of relativistic speeds summation is based just on
the translation of body’s uniform motion in the moving frame into the corresponding
motion relative to the resting frame. Actually, the statement of problem to find the
expression for summation of relativistic speeds Einstein wrote so: “Let
in the frame k moving with the speed v along the axis X of frame K,
the point moves according to the equations |
where w and w and w are constants. are constants.
Find the motion of point in the
frame K. If to the equations of point’s motion we introduce the values x,
y, z, t with the transform formulas introduced in the subsection 3 (trivial
Lorentz transforms – Sergey), we will yield |
[A. Einstein. On electrodynamics of moving bodies, vol. 1,
p. 20].
You can see, dear Vladimir, the course of solution in case
of body’s uniform motion is same as we applied in the problem of uniformly
accelerated motion. The law of body’s motion in one IRF is found same and we
substitute it to the Lorentz transforms to find the trajectory of body’s motion in
other IRF.
Relativists encounter difficulties in connection with
their postulate of constant speed of light. You could see, in this relation in the same
IRF, the 4-D interval is changed only because the accelerated body is present in this
frame. A very simple and natural question arises here – is the metric of space in
Relativity dependent on the fact that some bodies move in this frame inertially and some
other are accelerated? A "good" invariance of 4-D interval, I can say.  Let us think a while about the term ‘invariance’ – the absence of
variants in change. Well, some body accelerates – and interval in the IRF gains
another appearance: remains for inertial motions, while for accelerated motions we already
have to use new, special measures. This itself evidences that relativistic laws are not
equivalent, even for IRFs. We should not forget, when introducing relativity, relativists
specially emphasise that they define the metric of space through measurability with
measures resting in the related frame. If for some motions they have one measures and for
other motions – other, then measure as such is absent in Relativity, and all their
mathematics becomes senseless.
Let us think a while about the term ‘invariance’ – the absence of
variants in change. Well, some body accelerates – and interval in the IRF gains
another appearance: remains for inertial motions, while for accelerated motions we already
have to use new, special measures. This itself evidences that relativistic laws are not
equivalent, even for IRFs. We should not forget, when introducing relativity, relativists
specially emphasise that they define the metric of space through measurability with
measures resting in the related frame. If for some motions they have one measures and for
other motions – other, then measure as such is absent in Relativity, and all their
mathematics becomes senseless.
You also raised another important point – you mind
that my computations concern the low speeds (v << c). On one hand, I
already pointed you, as opposite to the relativistic version, in our problem we need not
this limitation. But I would like to draw your attention to one more important aspect.
When relativists considered the ‘uniformly accelerated’ motion, they undertook
not the trivial way but changed the concept of uniformly accelerated motion. The answer is
simple. See, in the Lorentz transforms, when they say that the body cannot exceed the
lightspeed, they always operate with expressions yielded in Lorentz transforms, but in the
initial frame there is no direct limitation. And if relativists operate with the concept
of uniformly accelerated motion in the accompanying frame, the meaning of uniformly
accelerated motion does not change because of it, and sooner or later the speed in that
frame will exceed the speed of light. Namely so relativists delete the momentarily
existing accompanying frames. It does not imply the limitation of speed in Relativity, as
even in the expression for summation of relativistic speeds, in case of one-way motion of
the body and moving frame, when the body reaches the lightspeed in this moving frame, we
yield |
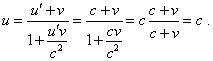 |
(d1.34) |
As we see, in (d1.34) the speed of intermediate frame v
has no limitations. The same we could find the speed of intermediate frame equal to the
speed of light, and according to the computations similar to (d1.34), the speed u'
or u could take any value faster than light. And, as we showed in our subsection 7.1.5, when the body and intermediate
frame move oppositely, the speed can develop up to infinity and change the direction of
body’s motion with respect to the speed of intermediate frame. Relativists impose the
limitations, considering the speed of body in the initial resting frame from the point of
moving frame, i.e. through the reverse operation. In this case the limitation is more
likely same ‘obviousness’ than rigorous proof that the speed cannot exceed the
lightspeed. Not in vain Einstein in the other his paper, “On the principle of
relativity and its corollaries”, considering the possibility of relative
faster-than-light motions, was already not so categorical: “The
speed v can take any value less than c. But if W > c, as we
premised, we always can choose v so that T < 0” [A. Einstein.
On the principle of relativity and its corollaries, vol. 1, p. 76], where T is the
time of transfer of signal between two points of frame. As we see, after Einstein, one has
also to select the value of frame’s speed, the body’s speed to be
slower-than-light. Einstein was sure, such selection is possible, but this is far from
being obvious, as this speed is given in the statement of problem and is not the subject
to select parameters arbitrarily.
Things look simpler with uniformly moving bodies, as their
speed does not vary in time. With accelerated bodies this ‘obviousness’ already
does not work, as the body varies its speed in time and we need not an illusory condition
of limit but a strong mathematical substantiation, which factually does not exist in
Relativity. It does not exist, because in the resting frame the relativistic kinematics is
taken to be identical to that classical. So relativists had to give up again their
postulates of invariant 4-D interval, in order to escape the faster-than-light speeds.
We see this feature in our case. The range in which the
solution (d1.18) is true can be found as follows: |
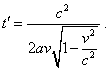 |
(d1.35) |
You see, there is no limitation, the speed to be little,
and according to the Lorentz transforms, up to this limit the body can accelerate without
any prohibition. The possible growth of mass can be the only relativistic argument. But
here they fall into their own trap. They have reduced dynamics to kinematics, while the
mass growth can be revealed in no other way than in dynamics. Before it, they yet have to
prove that in translation between IRFs, the conservation laws are true in Relativity.
Until they have not such proof, it appears that at the border defined by the condition
(d1.35), both speed and acceleration of the body in the moving IRF turn to infinity. And
this derivation is not limited by low speeds and accelerations of moving frame. To
illustrate, I graphed in Fig. 5 the variation of acceleration in time in the moving frame
for different values of speed of the frame itself.
|
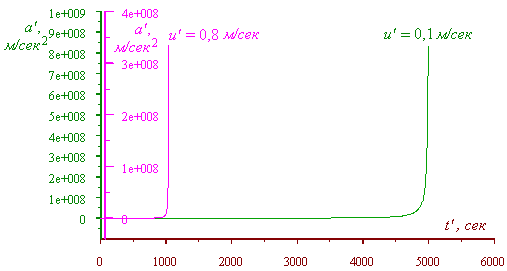
Fig. 5. The acceleration against time in the moving frame
for different values of frame’s speed and numerical value of constant acceleration in
the resting frame a = 0,001 c, m/s2
|
You see, the accelerations reach their limit simply at
different time, but the function fully remains its pattern.
VLADIMIR: However, attentively considering Fig. 3 and Fig.
5, I see that a = 0,001 c m/s2,
which is unclear. If c is just the c, the dimensionality is improper. Though
it also is near the ‘little’ speeds, this obviously is not the Newtonian limit.
SERGEY: I wrote the acceleration so for convenience,
meaning the dimensional coefficient of relation. Of course, this has no concern to the
relativistic record of acceleration as a dimensionless scalar value. So I everywhere said
of numerical value. I could write the full five-digit value of acceleration, but I
thought, such form is more visual, noting that the acceleration 10-time exceeding that of
free fall is critical for humans and instruments.
Concerning the Newtonian limit, this is a very indistinct
issue, because of errors which we agree to omit in calculations. Sometimes it is important
to be accurate to 5–7 decimal places, sometimes 1 % of error is very good, true? I
have chosen little values only to show that relativistic distortions remain at small
values of speeds and accelerations. At large speeds and accelerations all properties will
remain and when reaching the time limit, in all cases the speed and acceleration will turn
into infinity. Only the numerical values of parameters will change.
And if speaking of intervals within the lightspeed, the
acceleration will change in time as shown in Fig. 6
|
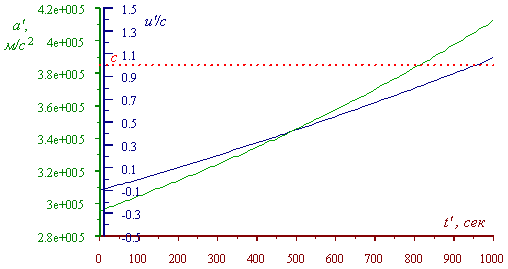
Fig. 6. The joined graph of variation of speed and
acceleration of the body in the moving frame, when uniformly accelerated motion in the
moving frame, at v = 0,1 c, m/s, and numerical value of
body’s constant acceleration in the resting frame a = 0,001 c, m/s2
|
As you can see from this graph, should the relativistic
conception were true, we might not apply the concept of uniformly accelerated motion in
the usual meaning even to thermal electrons being located, for example, in the field of
plane condenser, which would be immediately revealed in the simplest electron microscopes
and even in the cathode tubes.
VLADIMIR: You yielded quite paradoxical growth of
acceleration a' with growing t'. Maybe, it happened because except the
parameter (v << c), the parameter ? t'/v appeared in the solution.
With it, because of first condition, the value of parameter cannot much exceed 1. Well, if
we look at Fig. 3, we can see,
the considered range for t' much exceeds this condition. Though, we see a
monotonous function in the plot. I don’t know what to say of it. Is the classical
limit true for your (d1.21)?
SERGEY: It is senseless, dear Vladimir, to speak of
classical limit along with Relativity. The existing classical formalism, as you well know,
has not such limit, and when developed for high speeds, the limitation will appear without
any transformations of space and time and mythical growth of mass but because of correct
account of field dynamics. Dynamics! Not ‘dynamical kinematics’. 
VLADIMIR: As to the ‘mass growth’, we would have
to sort this matter out separately, dear Sergey. In SRT they obviously take the inertial
meaning of mass. But further, in other sections of theory, they postulate the
‘equivalence’ of gravitational and inertial hypostasis of mass. And
gravitational hypostasis reveals itself as the field, with all consequences. Though, it
hardly is worthy to develop this matter in this dialogue. Perhaps there is a sense to
consider it separately.
SERGEY: Indeed, and conclusions to which we will come in
this present dialogue, considering relativistic ‘dynamical kinematic’, will be
of great importance for this future dialogue. So let us go on, aren’t you against? |
Title
page: /1 / 2 / 3 / 4 / 5
/
|
|







