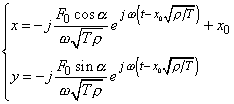14

S.B. Karavashkin

Each of these systems is similar to those considered in [1]. So we can write directly the exact analytical solutions for each of them, as follows:

for the x-component of vibration:

in the periodical regime ( < 1)

For the y-component of vibrations we yield relatively:

in the periodical regime ( < 1)

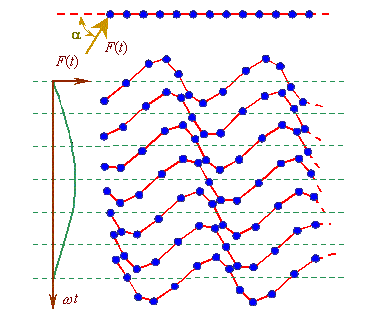
where = (²m/4s)^1/2 , = arcsin , _- = - (² - 1)^1/2 , F₀  is the amplitude of external force, n = 1, 2, 3, ... is the number of the studied element of elastic line, and is the circular frequency of affecting force.

As the result of superposition, there forms an inclined wave propagating with the positive axis x; this is corroborated by the vibration diagram shown in Fig. 2.

Fig. 2. Vibration in a semi-finite line under affection of the force inclined to the line axis. The line parameters: m - 0,01 kg,s = 100 N/m, a = 0,01 m, = 60^o, F₀   = 2 N, f = 15 Hz

Typically, the vibrations remain inclined pattern both with free vibrations in a lumped line and with the limiting process to a distributed line.

Basing on results presented in [1], the solution - e.g., for free vibrations - the sought solution will have the following form:

for the x- component of vibrations

where X_k and Y_k are the x- and y-components of vibration amplitude of the kth element whose parameters were specified, and k in this case is the number of element whose vibration was specified.

In case of limiting process to a distributed line we can present, like in [3],

where is the density; T is the line strain; x₀ is the distance from the line start to the point of rest of the considered line element. With it the solutions (3)- (8) transform into the following system:

This system describes parametrically an inclined wave propagation along the axis x, as is shown in Fig. 3.

Fig. 3. Vibrations in a distributed line whose start is affected by an external force inclined by the angle = 60^o