СЕЛФ

14

С.Б. Каравашкин и О.Н. Каравашкина

2. Сравнение экспериментальных результатов

Для выполнения поставленной задачи были использованы хорошо проанализированные экспериментальные результаты по исследованию ближнего ЭМ поля на длинных волнах, приведенные в обзорной монографии коллектива авторов под руководством Альперта [17, с. 836- 845]. В Главе VI, "Скорость радиоволн", исследуется закономерность изменения дополнительной фазы  * в ближней зоне источника поперечных ЭМ волн. Согласно выводам авторов, стандартная "…формула вертикальной составляющей электрического поля диполя… с учетом фазы волны имеет вид

где E _z - вертикальная составляющая электрического поля диполя;

W  - мощность излучателя в киловаттах;

 f() и соответственно модуль и фаза функции ослабления f();

- длина волны;

. - диэлектрическая постоянная земной поверхности. Однако формула (19) верна лишь на расстояниях r (4 5) от излучателя" [18, с. 837]. Иными словами, только в области, превышающей пять длин волн от излучателя, справедливо предположение о распространении длинных волн в волноводном слое между поверхностью и ионосферой, на основе которого была получена формула (19).

"Фазовая же структура электромагнитного поля и скорость радиоволн имеют … некоторые особенности именно на более близких расстояниях, примыкающих непосредственно к антенне. В этой зоне необходимо пользоваться для расчётов более сложной формулой, имеющей вид [19]

где k₂ =  k₁(')^1/2 =  k₁[ - i(4/)]^1/2 ;  - электрическая проводимость земли. Значения f() и вычисляются сложным образом с помощью рядов" [18, с. 837]. "Приведенные выше формулы относятся к случаю вертикального диполя, помещённого на поверхности земли. С приближением к точке излучения на расстояниях r 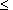начинает сказываться влияние конечных размеров антенны. Поэтому формула (20) становится непригодной для точных расчётов структуры поля. Строгих формул электромагнитного поля, учитывающих как конечные размеры антенны, так и конечную проводимость земли, не имеется. Однако анализ структуры поля вблизи антенны показал, что на этих расстояниях вполне пригодны формулы, выведенные для случая, когда проводимость земли принимается равной бесконечности. В этом случае фаза _z вертикальной компоненты E определяется выражением

[18, c. 838-839], где R₁ ,  R₂ , R₀ - расстояния до верхнего, нижнего и зеркального концов антенны соответственно, ₀ - т.н. укорочение антенны, т.е. отрезок, который дополняет длину антенны до /4.

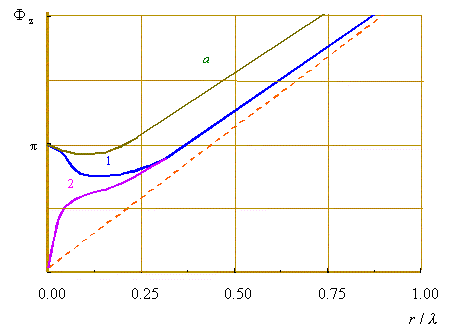
Рис. 3. Теоретическая зависимость фазы _z от r/ в ближней области антенны: 1 - антенна с удлинением при = ; 2 - антенна с укорочением при  = ; а - вертикальный диполь при = 1,7*10⁶ CGSE и = 4. [17, с. 840, рис. 122.4]

"Построенные по формуле (21) кривые зависимости _z от r/ для различных значений ₀ (рис. 3), иллюстрируют детали изменения фазы волны вблизи антенны; на этом же рисунке для сравнения приводится кривая _z, рассчитанная по формуле (20) для = 1,7*10⁶ CGSE и = 4" [18, с. 839].

Из представленного графика видно, что расчётные кривые, построенные по обеим вышеуказанным формулам, предсказывают конец ближней зоны в пределах r = , хотя, как указывалось самими авторами, область ближнего поля значительно больше. Другим недостатком приведенных расчётных кривых является плохое соответствие кривой а кривой 2, при одновременном хорошем соответствии этой кривой а кривой 1 в непосредственной близости к излучателю. Тем не менее данные построения показывают, что в ближней зоне ЭМ излучателя фаза не постоянна, как это следовало бы при отсутствии в этой области бегущей волны. Это дополнительно свидетельствует о неправомерности пренебрежения фазой запаздывания в ближней области, на что было указано в работе [11].