A BRIEF SURVEY OF RESULTS OBTAINED BY THE NEW NON-MATRIX METHOD This non-matrix method to obtain exact analyticlal solutions is quite young, it was founded at SELF in 1990 – 1994. To avoid errors and inaccuracy that have been introduced to the vibration theory by the conventional methods, we paid the principal attention to the sequential solving the problems, beginning with the simplest, as finite and infinite ideal homogeneous elastic lines, and progressing to resistant, heterogeneous, kinked, closed-loop systems, having different longitudinal and transversal stiffness coefficients etc. Although all investigated systems were up to now limited by one dimension, some of them, already solved, can be classified as two- or even three-dimensional. While many practically important models (see, e.g., [23], [27] and so on) can be and are reduced to 1D. The second task we have set when developing this method was the parallel investigation of lumped and corresponding distributed models. It enabled us to reveal operatively the features of these models and the transformation degree of solutions under the limit passing. It became easy feasible because of full determinacy of solutions with respect to line parameters and external action, as well as due to the analytically written solutions. Besides, these distinctions enabled us to check the solutions up by way of transition from the complex models to more simple, for which the solutions have been obtained before by a direct investigation. Indeed, the volume of solutions already obtained is quite wide and covers the practically entire complex of 1D basic models, so it is impossible to present them all here in the full measure. So we will concentrate not so much on the models themselves as on the vibration patterns distinctions revealed just due to the exact analytical solutions. The general solution for vibrant systems consists of three vibration regimes: |
|
periodical at the external force frequency |
|
aperiodical at |
|
and critical at |
|
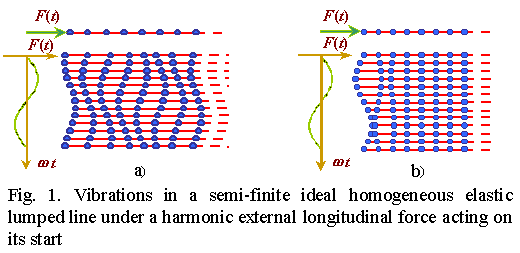
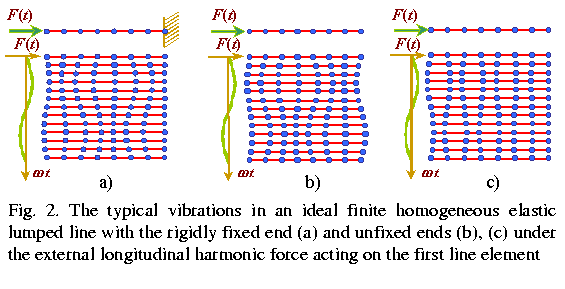
In Fig. 1, a and b, we show vibrations typical for periodical and aperiodical vibration regimes for a semi-finite homogeneous elastic line. One can see from the construction that the along-the-line anti-phase damping vibrations are inherent in the aperiodical regime. In other words, in this regime an elastic line behaves as an effective damper, despite the line is ideal and has not resistance. And anti-phase non-damping vibrations are inherent in the critical regime in a semi-finite elastic line. However, the critical and aperiodical regimes are inherent not in each model. For example, in an infinite line the critical regime is absent, and both regimes are absent with free vibrations in finite lines, but they both take place with free vibrations in infinite lines. Moreover, if in free vibrations in finite lines the discrete spectrum of characteristic frequencies is inherent and just this is revealed by the matrix techniques, in free vibrations in infinite lines the continuous spectrum takes place. The vibration pattern in aperiodical regime also has its salient features depending on the line model. If in infinite lines the damping obeyed to the power (not exponential) law with the base of power depending on frequency, in finite lines the damping distributes along the entire line with some variation of damping with frequency, though it has a complex-power pattern too. The same in critical regime. If in a semi-finite line the non-damping vibrations were inherent, in ideal finite lines also antiphase vibrations are inherent, but they damp linearly (see Fig. 2b). |
|
The exact analytical solutions reveal the important features of vibration pattern also when determining the phase characteristics. We said before that in some specific cases the indirect methods allow to obtain the exact analytical solutions. But the vibration amplitude and phase of some picked out (and as a rule boundary) element appear in them as the given parameters. It is impossible to obtain the solutions conventionally and analytically with the specifying parameters of an external force or moment. At the same time, as we see in Fig. 1a, the vibration phase of the elastic line first element does not coincide with the acting external force phase, but delays by some angle whose value depends on the elastic line parameters and frequency. At the limit passing to a distributed line this delay phase vanishes. This is why the solutions disagreement indicated by Skudrzyk [17, p.317] increases with the growing frequency. Applying the boundary conditions which were true for distributed lines to those lumped, we automatically lay a mistake into solutions, and it increases with the vibration frequency approaching to the critical. This is inherent in most types of elastic lumped lines. For example, in Fig. 2, a and b, the typical for periodical regime forced vibrations in finite lines with the rigidly fixed (a) and free (b) ends are presented. This is well seen in them that for a line with unfixed end the vibration phase delays from the external force phase by some value proportional to the line parameters and external force. When passing to the critical regime (Fig. 2b) the line vibrations become antiphase to the external force. The same with the boundary conditions for the second ends of a line. If for a rigidly fixed end the boundary conditions are obvious, on the unfixed end the vibration amplitude will not be maximal. In this case the boundary element vibration phase will also delay by the value proportional to the external force frequency. For simple lines these phases have a simple shape of a half phase delay with the wave propagation along the line, but in more complex models (e.g., having resonance subsystems, heterogeneities, kinks etc.) the analytical writing of these phases essentially complicates. To calculate them on the basis of regularities inherent in distributed lines is impossible. |