V.5 No 2 |
1 |
| Supplement 1 | |
|
|
V.5 No 2 |
1 |
| Supplement 1 | |
|
|
Supplement 1 Some additional aspects of the analysis of black hole conception S. B. Karavashkin and O.N. Karavashkina Special Laboratory for Fundamental Elaboration SELF 187 apt., 38 bldg., Prospect Gagarina, Kharkov, 61140, Ukraine phone +38 (057) 7370624; e-mail: selftrans@yandex.ru , selflab@mail.ru http://selftrans.narod.ru/SELFlab/index.html http://selftrans.narod.ru/index.html
After our paper was advertised, it was actively discussed on several forums. At the same time, as if in response to our notice about sensations for one day, NASA has disseminated a release that they have discovered 21 black hole at once, and globally recognised institutions confirmed this discovery true. In this connection, we thought necessary to add some details to our previous study and to analyse the NASA’s discovery.
Let us begin with the doubt of one colleague that Einstein grounded his GR not on the principle of equivalence of inertial and gravity mass but on the principle of equivalence of physical processes in inertial and non-inertial reference frames. True, in the page 14 of our work we analysed this issue quite enough and gave citations from Einstein and his followers. They all unambiguously state, under the principle of equivalence of inertial and gravity mass Einstein meant namely the equivalence of inertial and non-inertial reference frames. This principle is reflected also in relativistic modelling of processes. In particular, when Landau derives Schwarzschild’s metric, he points that he fully free substitutes the reference frame, irrespectively of, whether the frame was inertial or not. This we also mentioned in our study, in page 7. The same, Einstein in his work “The problem of particles in general theory of relativity”, doing not thinking of the physical meaning of introduced values, writes down in Schwarzschild’s solution a new value of radius [1, p. 428] as |
| (1) |
(we write this formula in the symbols used by Schwarzschild). With it, Schwarzschild’s solution takes the following form: |
| (2) |
“The new values g |
| (3) |
In such approach to the mathematical modelling, any
phantasmagoric solutions are possible, of course, but symbols introduced artificially
remain such and predestine the next difficulties. From this view, there arises a simple
question. Does there really exist Schwarzschild radius in the form in which it is
described by relativists - as some radius R = However strange it can seem with the abundant literature which more than 90 years was published on different versions of Schwarzschild’s geometry, with all generously funded projects in whose frames the astronomers attempt to reveal the celestial bodies whose substance to be compressed to this radius, - the answer to this question still is negative. Actually, the final Schwarzschild’s solution in spherical coordinates is |
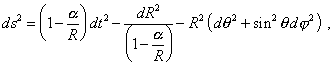 |
(4) |
where R is determined by (3). As we already said, this metric has a singularity at |
| (5) |
But R is not a measured parameter. As we also said above and as follows from the statement of problem in Schwarzschild’s derivation, the measured parameter is r. So (5) in the measured parameters will take the following form: |
| (6) |
and it follows from (3) that as the measured parameter r cannot be negative, the condition |
| (7) |
is strong. Due to this, in the really measured parameter, the singularity will take place in the centre, where the gravitating body is located, and the inversion of time will not take place at the so-called event horizon (5), since from the physical view, (5) determines the limit of existence of the parameter R, which at the same time is the limit of validity, where we may model the gravitating body by a physical point. While the abstract parameters, be they R or u, will remain abstract. Thus, the whole broadly advertised black hole conception appears only a consequence of incorrect transfer of abstract solutions into the real world. With it in the works by Einstein, Chandrasekhar and many other authors, in studying the singular Schwarzschild’s metric, we see already not a parameter R but symbol r, due to which we had to change the symbols in (1) and (2) to those Schwarzschild’s. Should we do not see this change but analyse exceptionally the developing course of thought, as most scientists do, traditionally relying on the author, then the virtual parameter R in leisurely fashion is transformed into the measured parameter r, and the virtual Schwarzschild’s radius takes the appearance of reality, remaining in its essence the same abstract. We strongly encountered it in discussing our paper on the forums. The colleagues appeared to be never able to grasp the difference in these parameters from the view of direct substitution due to which the virtuality substitutes reality. This is in order, as the very authors have put it as the underpinning to their theory: “The relativistic theory has to answer two questions: first, which is the mathematical nature of the field, and second, which equations has this field to satisfy ” [4, p. 725]. As we see, both aims which Einstein marked are the interpretations of mathematisation of physics, but among them one is absent - namely what differs the physics from other sciences - physics has to reveal the inner phenomenological essence of natural phenomenon. Without this target, which has to be the principal in physical studies, physics as the science unavoidably is emasculated into some virtual mathematical abstraction which produces phantasmagorias like black holes, craters of time, photon engines and so on. This relativistic substitution of reality by virtuality corroborates, when in the beginning of our paper we told of a ‘special’ relativistic mathematical approach, we had no wish to discredit some particular scientists or a conception which they develop, we only showed things how they really occur. To surmount these difficulties, relativists have only two ways: either, retaining the formalism of conventional conception, to build a new GR system free of Einstein’s equivalence principle and consistent in the abstract parameters introduced together with those measured, which is practically impossible - or to deny Einstein’s construction as erroneous. Of course, both ways are inadmissible for relativists, but regrettably, there exists no third way in frames of scientific honesty. It is impossible to prove physical laws equivalent in inertial and non-inertial frames in limits of correct physical logic and methodology of physics, as they are non-equivalent in principle. ”Application of non-inertial reference frame is determined by the given type of problem. … Of course, the acceleration of point caused by non-inertiality of reference system with reference to this system is quite real, despite there exist other, inertial reference systems, with respect to which this acceleration is absent. In the equation (for non-inertial reference frame - Authors) the acceleration was written so as it were caused by some additional forces usually called forces of inertia. As opposite to interaction forces, inertia forces are proportional only to the mass of each body to which they are applied. This is natural, as the accelerations caused by non-inertiality of the system are same by definition for bodies placed to the same point of the system and moving in it equally. The term ‘force’ is applied to it, because the corresponding expressions are proportional to the product of masses by acceleration” [27, p. 75]. We in our paper quite completely showed these features on the example of a body moving with respect to a freely falling non-inertial frame. We can add to it, not always the observer whose motion is considered from the view of non-inertial frame will feel the inertia forces. In particular, if the observer moved uniformly and rectilinearly, from the view of additionally introduced non-inertial reference frame, it will move nonlinearly, and from the view of nonlinear frame, it will be affected by some forces of inertia. But factually these forces will not affect the observer, although we have to account them in calculation in nonlinear frame. We can determine these fictitious forces exceptionally by way of matching the laws of motion in inertial and non-inertial frames. How these fictitious forces will be accounted, will depend on the pattern of acceleration of non-inertial frame. For example, in the problem of observer’s motion in gravity field from the view of non-inertial frame, the forces caused by his interaction with the gravity field will be real for him. But the forces caused by non-inertiality of the frame will be fictitious for the observer. Such situation leads us to the fact that from the view of non-inertial frame, the observer will be initially attracted to the gravitating centre and then as if repelled. We can reveal which forces are real, only passing to the inertial frame in which there are considered only forces really acting on the observer and are added no forces related to the nonlinearity of frame motion. Just so we in the main paper pointed that classical mechanics strongly prefers the inertial frames. “Basing on the equality |
| (a) |
we can easily show, why Newton equations have similar appearance in all inertial reference systems. The interaction forces depend on the relative coordinates of particles, so they remain unchanged in transformation (a), since the common summand Vt is reduced in the argument of any function which contains the coordinate difference. In the left part of Newton equation the accelerations, i.e. the second derivatives of coordinates over time, are involved. But as the time is involved to (a) linearly and in both systems is equal by the main supposition, |
Consequently, the equations of mechanics have an identical appearance in any inertial reference systems. Otherwise it is done to say that the equations of mechanics are invariant in relation to these transformations which are usually called Galilean transformations” [27, p. 73]. In non-inertial frames such invariance in general case does not occur because of time-variable motion of the frame. |