V.5 No 2 |
7 |
| Supplement 1 | |
|
|
V.5 No 2 |
7 |
| Supplement 1 | |
|
|
While the x-coordinates determined by the condition of transformation from spherical coordinates as [2, p. 201- 202] |
| (32) |
can be linear at no conditions because of nonlinearity of x1 and x2 . The more that the nonlinearity of these coordinates is worsened by nonlinearity of metric in these coordinates [2, p. 202]: |
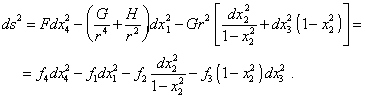 |
(33) |
From (33), even without finding the coefficients F, G, H, we see that at one of boundaries of domain of existence, the metric is singular in x2 at |
| (34) |
Or rather, under condition (34), in spherical coordinates the singularity will be absent. Actually, |
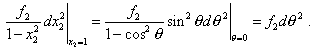 |
(35) |
But in the x-metric where we do transformations this singularity will take place and we have to account it, the more, when the matter is of linear element namely in this metric. At the second boundary at |
| (36) |
the metric in x2 is finite and two-valued, as it is two-valued in the whole domain of existence except (34). By the way, namely under condition (36) Schwarzschild sought his solution, premising, it has to determine the equatorial plane - this means, “due to the symmetry about turns, it is sufficient to write down the field equations only in equatorial plane (x2 = 0)” [2, p. 203]. Factually, as we see from (36), Schwarzschild’s condition determines polar regions, and because of two-valued metric - both regions at once. Thus, Schwarzschild’s differentiation in these regions is quite doubtful or at least needs to be additionally substantiated, - just as the symmetry about turns in x2 in so nonlinear metric. Well, even doing not touching the phenomenology of processes which Schwarzschild describes, we see in his derivation quite many fogged violations of mathematical formalism, which allowed him to yield convenient solutions. At the same time, the above study shows that Einstein’s statement of possibility to pass from Minkowski’s metric (13) to generalised metric (15) also is invalid and limited by the class of metrics (19), which he presented. But the metric (19), just as the initial Schwarzschild’s metric (23) with the absent last summand in the right part (the expression (31)), has basically other solution, which causes no singularity at some distance from the centre of point gravitating body. This proves, Schwarzschild did not elaborate the issue, whether he might use the metric (23) in modelling of processes in gravity field in frames of relativistic conception. We have to mark here that in order to check, we could take not initial metric used by Schwarzschild but the metric used for a similar problem by Landau or Chandrasekhar. In all cases, in attempts to put these metrics in agreement with the condition of local conservation of Lorentz transformation, we would yield the same inconsistency as in case with Schwarzschild’s rectilinear metric. Such things occur in Relativity enough often, when the scientists approach to modelling mere formally, doing not taking into account the whole amount of features and mathematical causation, which the equations have to satisfy even in narrow limits of relativistic conception. In particular, in the beginning of his work, Schwarzschild correctly pointed the condition formulated by Einstein: “The solution is (spatially) symmetrical with respect to the coordinate origin in the sense that, if we make the linear orthogonal (spatial) transformation of coordinates, we will yield again the same solution” [25, p. 441]. But how Schwarzschild interpreted this solution? In passing from rectangular coordinates to those spherical, he writes: “With it, the element of volume in spherical coordinates is equal to |
| (37) |
so that the Jacobian of transformation from old coordinates to those new that is equal to |
| (38) |
differs from the unity [2, p. 201]. But what concern has here the Jacobian equal to the unity? If Schwarzschild premised it from the view of spatial symmetry of the metric, the equality has to be determined in limits of turns of initial metric. In passing from one coordinate system to another, even in frames of classical analytical geometry, the Jacobian will not be equal to unity, or the meaning of Jacobian would be lost. If we premise that it has to satisfy the condition for determinant, which Einstein also pointed, |
| (39) |
it is determined not in passing from one coordinate system
to another, but from the condition of conservation in Lorentz transformation which we
showed above, i.e. from the transformations in the local metric in which, after
Einstein’s though, the invariance of 4-interval has to remain. Or rather, we to be
exhaustively exact, Einstein derived his (39) proceeding from some other consideration: “If we premise the substantiated in the last work ([26] -
Authors) that the scalar of tensor of energy of ‘matter’
is always zero, then there is added the condition (39)” [25, p. 440]. Here
Einstein meant under the word ‘matter’ not some weighty matter but just the
aether with whose materiality he had to agree in developing his GR. He himself confirms it
when proves this premise: “the
hypothesis that yet has to be justified concerns the following: from the tensor of energy
of ‘matter’ T |
| (40) |
We well know that for electromagnetic field this scalar turns to zero. On the contrary, for the matter as such it apparently differs from zero. But if we consider as a particular example, e.g., a liquid, then usually (neglecting the pressure (! - Authors)) it is supposed that |
| (41) |
so that |
| (42) |
Consequently, in this case the track of energy tensor does not turn to zero” [26, p. 435]. But in [25] Einstein considers not electromagnetic but gravity field. If in his work “Ether and the theory of relativity” Einstein states that “in accordance with general theory of relativity, space is inconceivable without ether; actually, in such space not only light propagation would be impossible, but scales and clocks could not exist and there would be no space-time distances in the physical meaning of the word” [16 p. 689], then in [26] it sounds otherwise: “In accordance with our knowledge (? - Authors), we should not think ‘matter’ as something initially given, physically elementary. Still there are many people hoping that it will be possible to reduce the matter to mere electromagnetic processes, but these processes would anyway occur, according to the theory improved in comparison with Maxwell’s electrodynamics. Suppose for a while that in the electrodynamics improved so, the scalar of energy tensor would also vanish (? - Authors)! Would then the just-yielded result prove that in such theory we couldn’t yield the matter? I think, we can answer this question negatively, as then it would be quite possible that the essential component of ‘matter’ to which the just shown expression relates is gravity fields. In such case, although it could seem that the value (40) is positive for the whole system, in reality only the value |
| (43) |
is positive, while (40) vanishes everywhere. Further we will premise that the condition |
| (44) |
actually is true always” [26, p. 436]. |