SELF |
16 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
16 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
While the essence remains such. Having unfoundedly
equalised phenomenologically inertial and non-inertial reference frames, Einstein
inevitably came to violation of conservation laws established by classical physics. But to
the detriment of the phenomenology of laws of nature, juggling with the terms and symbols,
he renounced the conservation laws for the sake of retaining the virtual principle of
relativity for non-inertial frames. Initially he made so secretly, having substituted the
appearance of tensors, but finally came to an explicit substitution, introducing the term In the paper "The issues of cosmology in general theory of relativity", before to introduce his novelty, Einstein, by his custom, forewords it by quite doubtful refutation addressed to Newtonian theory: "If we apply to the stars the Boltzmann's law of distribution of gas molecules, considering the stellar system as the gas in stationary thermal motion, it appears that Newtonian universe could not exist at all, because to the finite difference of potentials corresponds the finite ratio of densities. Consequently, the zero density at the infinity causes zero density in the centre" [40, p. 602]. Is not it a brilliant conclusion? By an analogy with it we might conclude, if in the field of charged body there exists a finite difference of potentials between some point of the field and infinity, the zero potential at the infinity means zero field in the finite region of charged body. None the less, just relying on the mentioned 'difficulties' of Newtonian theory, Einstein undertakes its modification. "For it we first of all will show the way which we should not take too seriously (! - Authors), as it serves only to grasp better the following consideration. Instead Poisson equation we will write |
| (63) |
where |
| (64) |
is the solution of equation (63)" [ibidem]. There arises the question: well, in case of inconstant mass, (63) satisfies the conservation laws? Of course, no, and the very fact that in order to put into agreement his transitions to the non-inertial reference frame, Einstein had to give up the conservation law, says that in inertial and non-inertial reference frames different laws are true and all solutions yielded in non-inertial frames without a provided law of transition to the inertial frame, beforehand stipulated for each specific problem, are wrong. This was multiply corroborated by the experimental practice. And Einstein understood it distinctively, as well as he understood, how artificial is his 'innovation' from the view of physics. Just so he cautiously did not emphasise the meaning of his 'innovation'. As concerns to the non-uniform distribution of density,
Einstein also made off quite openly: "If we now suppose that
there are local (? - Authors) inhomogeneities in the matter
distribution that do not change the average density of distribution, to the constant value
(64) of the potential After all reservations Einstein returns to his initial equation of gravity field in another way: "The equations of gravity field which were suggested by mine for an arbitrarily chosen reference frame have the following form: |
| (65) |
… The system of equations will never
be satisfied, if instead g |
| (66) |
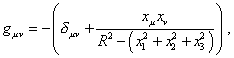 |
(67) |
and instead (the contravariant) tensor of matter of energy - the value |
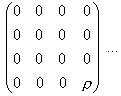 |
(68) |
But the system of equations (65) admits (? - Authors) one quite simple
generalisation compatible with the postulate of relativity (? - Authors) and fully similar to the above given as (63) generalisation of Poisson
equation. Actually, to the left part of field equation (65) we may (? - Authors) add the fundamental tensor g |
| (69) |
[40, p. 610- 611]. Comparing this 'technique' to solve of problem of general covariance with the considered before techniques to solve the problems of collapsing bodies, we clearly see the common approach typical for all techniques of solving in relativistic formalism. This technique is based on retaining of one and the only principle - geometrisation of all physical processes in the nature on the basis of outward similarity in separate cases specially chosen for this comparison. And we have to underline, this is based namely on the principle of wholesale geometrisation, not the relativity principle, as relativists wish to assure us all. In order to achieve this aim, they equally easy can establish the constant light velocity for all reference frames - and immediately deny it, deny the existence of whatever material substance between the material bodies - and immediately admit the physical properties of this absolutely void space. They can turn to zero all tensors of energy-momentum and retain non-zero some tensor convenient for them. They are even ready to give up the conservation laws, telling, this is the struggle for general covariance. They are able to state that the laws of nature in inertial and non-inertial reference frames are equally true, if they need it to achieve their geometrical representation of physical processes. By this reason, by paradoxical contradiction, mathematics in relativistic methodology is fully deprived of the title The Queen of Proof, as the formal logic on whose basis such or other thesis is proven in classical mathematics is intolerable to such arbitrariness as relativists need to achieve their aim. This is why we have to speak of geometrisation of the world in relativistic methodology with the same reservation as for all relativistic mathematics. In that number in differential geometry they use only those aspects which, in separation from other interrelated parts, allow the arbitrary interpretations. From the mentioned part they also have extracted only those principles and transformations which were advantageous for them. We in this study did not touch these issues, but we can mention in a general line, how arbitrarily they treated with the operation of convolution, choice and transformation of metric and much other. R. Penrose exactly described the essence of their approach to the operations with tensors and metrics: "When the physicist used the values <<gab>> either <<R abcd>>, I do not think that he often means in it the set of components depending on the choice of frame; he rather means a physical object independent of the coordinate system which embodies these components. Furthermore, the method of indexes allows to make conveniently some algebraic operations leading to new objects, and these operations really in no way depend on the choice of frame. In essence, these algebraic operations are extremely simple, but at the same time flexible, with their help we can execute more complicated operations. It would be rather disappointed to refuse such powerful and flexible method only because of somewhat awkward feeling caused by the condition of summing and by the dependence on specific choice of vectorial basis … We will save our time and efforts, abstaining from extreme formalisation" [41, p. 33- 34]. With it, quite natural result is the complete absurdity of obtained solutions and absence of whatever physical associations with real processes of nature, which seems to be not hurting them. But it must hurt all those who tries in their studies to reveal the real essence, not to follow the target of their own phantasmagorias. We made this study to show it. Of course, it could not cover the whole amount of issues with which relativists juggle. We concentrated on the main trick which they use. Knowing and understanding this, we can much easier understand in each specific case the layering of false theses and juggling with mathematical formalism - the ways in which relativists substantiate their unphysical approaches and pseudo-mathematical solutions. This is the main value of the presented study. Supplement 1. Some additional aspects of the analysis of black hole conception |
Contents: / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 / 16 / 17 /