SELF

8

S.B. Karavashkin and O.N. Karavashkina

4. Phenomenological discrepancies in relativistic solving the problem of collapsing dust-like sphere

The same as in Schwarzschild's problem, in the problem of collapsing dust-like sphere, the relativists use their conventional methods. Having established for the sake of outer reference to the physics of process that "in centrally symmetrical case, the field equations can be solved in general form, with neglect of substance pressure, i.e. for the equation of state of 'dust-like' matter: p = 0  (R. Tolman, 1934)" [23, p. 400], Landau immediately writes the metric equation for this problem:

doing not care a least, how much (43) is consistent with real processes taking place in a dust-like cloud, as well as, this metric is nonlinear and describes the non-inertial reference frame, in which all laws of dynamics are violated. None the less, for relativists this is of no importance. Furthermore, on the basis of (43) he finds the components of Ricci tensor; they lead him to some kind of Einstein equations.

Solving these equations, Landau derives some amount of solutions

where f (R) is an arbitrary function satisfying only the condition 1 + f > 0 , F (R)  also is some arbitrary function, and   is the parameter in the parametric representation.

And these solutions, where still are absent real physical processes in the dust-like sphere, are analysed for the condition of collapse in space and time. There appears that "the limiting pattern of metric inside the sphere at ₀ (R) is the same in all three cases

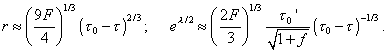This means, all radial distances (in the considered reference frame) are tending to infinity, and circular - to zero, and all volumes are also tending to zero (like  - ₀)" [23, p. 404]. True, Landau makes here a reservation: "The fact that in the considered solution the collapse arises at any mass of sphere is a natural consequence of pressure neglect. It stands to reason that at the supposition of dust-like substance is irrelevant from physical view and we have to use the ultra-relativistic equation of state p = /3. But it appears that general character of limiting laws of compression is to a considerable extent independent of the equation of state of matter (see E.M. Lifshitz and I.M. Khalatnikov. Journal of Experimental and theoretical physic, 39, 149, (1960))" [23, p. 404]. But this reservation already means that the initial modelling equation, built on the stipulation of free fall of matter onto the centre with the growing pressure, loses its validity - of course, if for the sake of planned result he will not neglect any factor preventing the target. While the factors related to pressure caused by the matter compression are not so insignificant, Landau to be right brushing it aside. On one hand, it is right that "at very high pressures the compressibility of matter does not depend on its individual properties, i.e. on the structure of electron shells of atoms" [25, p. 506]. At the same time, the experimentally traceable regularity of the specific variation of the volume of substance V / V  with growing pressure shows a clearly logarithmic dependence - we can make sure in the diagrams for liquid and solid bodies shown in Fig. 2.

a                                                                               b

Fig. 2. The compressibility of liquids (a) and solid bodies (b) after P. Bridgman: 1 - n-pentane, 2 - ethyl alcohol, 3 - water

The pattern of gases compressibility also does not inscribe into the model of possibility of free fall onto the centre of gravitating mass. "The gases have high compressibility at the pressure about hundreds of atmospheres; it considerably descends as the pressure grows, when the density of compressed gas becomes comparable with the density of liquid (at 10 000 atmospheres and 50^o C, the density of nitrogen is equal to 1,12 g/cm³). At several thousands of atmospheres, the properties of gas and liquid become so similar that we can determine the gas compressibility through Theta equation for compressibility of liquids

where V₀ and p₀ are initial, and V and p - final values of the volume and pressure, and C and B are constants." [25, p. 505- 506]. As we see, (47) also describes the exponential growth of pressure with decreasing volume of substance. To prove the importance of pressure, it is sufficient to show the orders of pressures that arise in a body compressed under affection of gravity forces.