SELF |
6 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
6 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
Actually, basing on four conditions formulated by Einstein for a gravitating field: " 1. All components have to be independent of time x4 . 2. The equalities g 3. The solution has to be symmetrical in the space around the coordinate origin, i.e., to pass to itself in orthogonal transformation of coordinates x1, x2 , x3 (rotation). 4. At the infinity, all values g |
[21, p. 200], Schwarzschild, without long pondering, introduces the metric as follows: "If we denote the time as t and rectilinear coordinates as x, y, z, it is obvious that the most general linear element satisfying the requirements 1- 3, is the following: |
| (14) |
here F, G and H are the functions of value r = (x2 + y2 + z2)1/2 " [21, p. 201]. From (14) we see that Schwarzschild, on the basis of standard rectilinear coordinate system, introduced some nonlinear metric, in which the measure of length along each axis changes along the axis, and time at each point of such reference frame depends in some way on the radius-vector. A simple question arises: which are the grounds to introduce the metric namely in such form? Maybe, this is stipulated by equations (12)? No, Schwarzschild yet did not come to them, he will operate with them later. Maybe, the condition (3) of spherical symmetry in space stipulated it? Also no, and the next step of solving shows it. At that step Schwarzschild passes to the spherical coordinates through the standard formulas of orthogonal transformation |
| (15) |
With it he comes to a new, also nonlinear metric |
| (16) |
"With it the element of volume in spherical coordinates is |
| (17) |
so that the Jacobian of transformation
from old coordinates to those new is equal to r2sin |
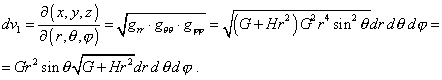 |
(18) |
Thus, introducing the transformation |
| (19) |
as the next step, Schwarzschild already could not satisfy the equality |
| (20) |
because he had to satisfy another equality |
| (21) |
But if, violating the equality of Jacobian to the unity, Schwarzschild dared to transform (19), he at once felt into a next violation of mathematical formalism that stretches from the very beginning of derivation. When he introduced a new nonlinear reference frame (19), his metric took the following appearance: |
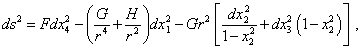 |
(22) |
or, with account of introduced substitutions, |
| (23) |
From (23), given the condition which Schwarzschild wrote to determine |
| (24) |
Schwarzschild comes to the system of equalities determining f1 , f2 , f3, : |
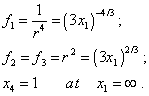 |
(25) |
But from the yielded extensions of definition (25), we can, without finding the field equations, immediately determine two initial parameters G and H . Actually, with account of (22) and (23), the second equality in (25) can be written so: |
| (26) |
hence |
| (27) |
Given (27) and again (22) and (23), we yield on the basis of first equality of (25) |
| (28) |
from which immediately follows |
| (29) |
Now with account of (27) and (29), the initial metric (14) takes a very simple shape |
| (30) |
which needs neither further finding of field potentials nor so unobvious transformations in nonlinear and non-inertial reference frames, nor the very transitions to non-inertial reference frames. And the result which we yielded is unambiguous and predictable, as it was given by the condition determining the determinant with which Schwarzschild operated. Equation (30) is fully identical to Minkowski metric for void space, the only difference is the undetermined metric tensor |
| (31) |
Contents: / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 / 16 / 17 /