V.5 No 2 |
7 |
| On reality of black holes | |
|
|
V.5 No 2 |
7 |
| On reality of black holes | |
|
|
But Schwarzschild did not understand that the redetermination (25) already cleared the metric spatial tensors of metric (14) which he gave a priori. Having gone quite long way to find geodesics in the yielded nonlinear and non-inertial reference frame, he yielded another result, which has been taken by relativists as a significant achievement of relativistic thought. Schwarzschild represented this result as follows: "thus, the complete solution of the stated problem is |
| (32) |
where R is the ancillary value: |
[22, p. 205]. It is easy to see that yielded solution (32), although it satisfies the condition for determinant (24), does not satisfy the equations (25) which were the underpinning of the following Schwarzschild's transformations from (25) to (32). And from (32) naturally follows also the solution different from (30) that was yielded on the basis of (25). These discrepancies in results, immediately following from (25) and obtained after relativistic manipulations with geodesics and Einsteinian tensor of energy-momentum, tell only that the manipulations are erroneous. None the less, despite so deep discrepancies in the very derivation of Schwarzschild's solution, namely this solution (32) relativists have taken as the basis of black hole theory, as it contained a singularity at a non-zero distance from the centre of gravitating body location. That solution had a form |
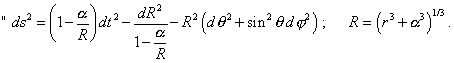 |
(33) |
One constant At the same time, even an outward phenomenological analysis shows that with correct mathematical approach, the solution (33) basically could not be yielded. The problem was solved for a point stationary source of gravity field of Newtonian type, i.e. for the source in which the singularity has to take place at the point of location of the very source. He introduced no additional factors able to shift this singularity from the centre to some radius, therefore the solution (33) could not be a result of author's incorrect mathematical operations, and the analysis showed it. We have to add to it that the next derivations of Schwarzschild solution undertaken, in that number, by Hamilton [1], Landau [23] and Chandrasekhar [24] already do not contain Schwarzschild's transformations and stipulations. In particular, Landau in his interpretation of Schwarzschild's derivation was exceptionally straightforward and felt free in choice of transformations and in neglecting the physical meaning of processes, when introduced his metric in the appearance immediately like the spherical (16): |
| (34) |
where a, h, k, l are some functions of the 'radius-vector' r and 'time' t " [23, p. 381]. In relation of coefficient l(r, t) he at once violates the second condition by Einstein: |
| (35) |
have to be strongly true with |
| (36) |
where f1, f2 are any functions of new coordinates r' and t' . Taking this opportunity, let us choose r
and time t so that, first, the coefficient a (r, t)
at drdt in the expression for ds2 to vanish and, second, the coefficient k
(r, t) to be equal simply to -r2 (these conditions yet do not define
the unambiguous choice of time coordinate: we still can impose on it any transformation of
the type t = f (t') that does not contain r).
This last means that the radius-vector r is determined so that the length of
circumference with the centre at the coordinate origin to be equal to 2 |
| (37) |
[23, p. 381- 382]. As we see, Landau has omitted all the initial part of
Schwarzschild's derivation. He begins to solve in fact from the place where Schwarzschild
already has mistaken. And also, we hardly can call a derivation this arbitrary choice of
the form of coefficients. This is rather a way to avoid a difficult place of
Schwarzschild's derivation than an independent derivation. And the equation (37) basically
differs not only from (16) but from (23), too, which required from Landau some additional
efforts and unobvious redetermination of |
| (38) |
but having made a substitution |
| (39) |
[24, p. 98]. As the result for the new type of metric |
| (40) |
which is not a direct transition from (38) to (40), he also found necessary to give the desirable type of metric coefficients ad libitum: "If we introduce the designations |
| (41) |
the metric will take the form |
| (42) |
[24, p. 98]. As we see, Chandrasekhar the same forcedly
and non-mathematically transforms the metric to the form convenient to yield the result
desirable for relativists, avoiding the difficult place of Schwarzschild's derivation.
This is standard for relativistic 'mathematics', in which the problematic places are
passed not by way of thorough analysis of phenomenology but by giving the desirable
relationship ad libitum. Landau does not care a least, for example, how much rightful is
his following record: "Meaning under x0, x1, x2, x3 accordingly ct, r, None the less, multiple contrivance and application of force in mathematics are unable to solve the main difficulty - to make the solutions consistent with the phenomenology. In this case, as we said above, Schwarzschild's problem was solved for the outer area of stationary point source of gravity field. Even without so long and unobvious transformations in non-inertial reference frames, it is seen on the basis of simple straight solutions built on Newtonian gravity potentials that the singularity cannot be out of the centre of the point gravitating mass. All the rest is an artificial trick in striving to the 'necessary' result. With such mathematical approach, there is no surprise that in further development of black hole theory, relativists apply Schwarzschild's solutions, without any serious changes, for gravitating body having final radius. Now there are considered already the conditions inside the gravitating body under Schwarzschild's sphere. For relativists this is quite natural 'application' of mathematics, when not the logic of stipulations but logic of convenient personal choice shows the solution. True, this immediately reflects on the solutions, but the practice shows, relativists do not care. Having formulated - or rather guessed some scientific-like way, they make a fetish from the result and are ready to rewrite the proof, to change the stipulations, to choose arbitrarily again and again the type of equations and relations, but they strongly keep the result. This concerns both particular and general issues. Specifically, as we saw in previous item of this work, Einstein, passing to GR, fully denied the initial postulates of SR, but with it he retained the symbol of relativistic space-time transformation, promiscuously confusing both the formulas of SR and new formulas of GR. So we see, the manner to solve in frames of relativistic 'new mathematics' basically differs, indeed, from the logic and stipulation of proof, which is inherent in classical mathematics and which has elevated the mathematics to the rank of queen of proof. Relativistic mathematics took the place of some obsequious servant that executes orders in limits of orders. But in such case mathematics already is not an argument of proof, even if the text of proof was abundant of formulas and substitutions. The more that it cannot now generalise or predict results on the basis of modelling of physical processes. This function took now he who applied the force to the proof of regularity of his interest. And the responsibility is now lifted from the mathematical formalism and put on him who, with the help of pressure in science, attempts to prove what he wants, not to study what he yields on the basis of independent and unbiased modelling. Such tricks of force, of course, led to the situation of which worried Feynman, when in presence of beautiful laws, the solution does not 'join'. We will prove it in many discrepancies that follow from Schwarzschild's solution of force. |
Contents: / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 / 16 / 17 /