SELF |
6 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
6 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
In this connection we would like to touch one more question from the Russian-language Astroforum. In discussion on the main paper, one colleague removed all its physical aspects and concentrated his attention on a narrow issue of mathematical mistake made by Schwarzschild in derivation of his final formula (4). We can mark as the merit of this colleague, he did not confine himself to some doubtful relativistic literature which is exceptionally abundant now. He, just as we do, addressed to the primary source and was right: in our derivation of coefficients (25)- (30), we did not take into account Schwarzschild’s conditions at which our expressions will be true. Actually, these expressions will be true namely at the infinite distance from the gravitating body, as Schwarzschild pointed. However, there are more mistakes in Schwarzschild’s derivation. In our paper we did not rise the full amount of these mere mathematical mistakes, but now, as it became the matter of principle, we will add to Schwarzschild’s basic mistake, mentioned above in this Supplement, some aspects which we did not touch in the paper in order to retain more clear the main line of our study. Let us see the initial equation on whose basis Schwarzschild developed his mathematical tool. This is the equation of metric in the rectangular coordinates [2, p. 201] |
| (23) |
In order this metric to satisfy Einstein’s conditions, it has to be reducible to Minkowski metric in any local region of space. As in all works on SR just rectangular metric is used and invariance of light speed has to be true in any inertial metric, the metric (23) has to satisfy locally the SR postulates. Premising so, assume F, G and H to be constant values. To begin with, let us draw our attention that these coefficients have different dimensions. If ds is measured in metres, F is measured in metres2/s2, G is dimensionless, and H is measured in metre -2. Can, e.g., F become also dimensionless, if we introduce the light speed under the sign of differential over time? Unfortunately, no. As we saw above, Einstein admitted that the light speed is inconstant in gravity field and depends on spatial coordinates. So |
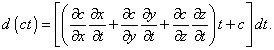 |
(24) |
It follows from (24) that, inserting the light speed under the differential, we make the time dependent on spatial parameters. With it the rule of differentiating which Schwarzschild used in his derivation will basically change and the solution will be basically other, if it will be at all under such conditions of differentiation. Here we have to point the reason of so complicated differentiation. The matter is, in general case, if we displace some trial body along the trajectory ds, in the beginning and in the end of trajectory the speed of light will be different. This will naturally affect the differential dt, despite the time itself may be independent of spatial coordinates. Due to the said, if we take the parameters of location in the beginning and in the end of infinitesimal interval ds and operate in full accordance with the rules to find the total differential, we will come to (24). But as Schwarzschild did not account the dependence of time parameter on spatial coordinates, we have no right to introduce the light speed under the sign of differential. Further, to make most general check of mathematical correctness of solution, we will compare the physical dimension with the finite Schwarzschild’s solution and then will go on. The finite values of coefficients as Schwarzschild found them are |
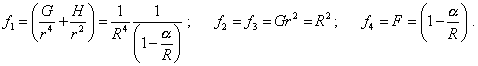 |
(25) |
From (25) we immediately see that the dimension of solution for G and H coincides, but for F does not. This parameter is dimensionless, which can be only in case if the light speed is under the differential. But, as we showed it above, the computation will have with it basically other appearance. Thus, even doing not deepen into the very computation, we can tell, Schwarzschild’s derivation is physically incorrect. Further, consider the initial expression (23), how it satisfies the local conditions of SR. The determinant of this metric will be |
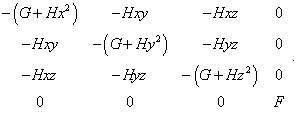 |
(26) |
It is easy to see from (26) that the interval (23) even in local case of permanent potential will not conserve but will change with respect to the direction of coordinate axes, which doubts the consistence of the metric conveniently chosen by Schwarzschild to the task of modelling. To show this discrepancy more distinctively, we can go farther, premising, as Einstein did, that SR is true under local conditions of constant coefficients F, G, H. For it, suppose that there exists one more (dotted) reference frame with the same metric (23), which moves along the axis x with respect to this frame. If the light speed in the local meaning conserves in this metric, then, applying Lorentz transformation to (23), we have to yield the same determinant (26). To pass, we have to note that in (23) there are both differentials of spatial coordinates and time and coordinates as such. So, to facilitate our study, we have additionally to premise zero initial conditions when integrating Lorentz differential transformations. These transformations will take the following form [24, p. 232]: |
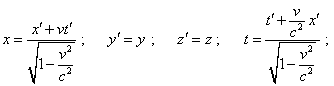 |
(27) |
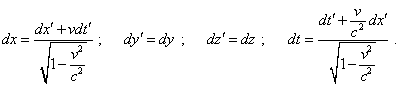 |
(28) |
Substituting (27) and (28) into (23), yield |
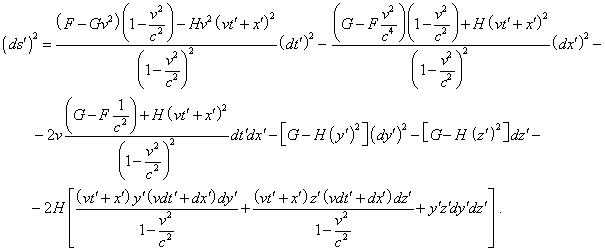 |
(29) |
Comparing (29) with (23), we will easily see after three first summands of the right part of (29) that the metrics will be equivalent exceptionally under condition |
| (30) |
i.e. under condition very close to that which we yielded in our paper - that the metric used by Schwarzschild will retain its local invariance of 4-interval defined by Einstein, only under condition of zero H. Additionally, G and F / c2 have to be equal. As the chosen local region is arbitrary, (30) has to be true in the whole space surrounding the gravitating body. With it, the determinant of metric will be automatically reduced to (20) shown by Einstein, and the initial equation in Schwarzschild’s derivation will be |
| (31) |
This expression is easy to transform into spherical coordinates, it needs no special x-coordinates which Schwarzschild thought out. And (31), not Schwarzschild’s coordinates, will be linear elements which Schwarzschild sought, outlining the target of his study as follows: “The task is to find the linear element with such coefficients, which would satisfy the field equations, condition for the determinant and four listed requirements (Einstein’s - Authors)” [2, p. 200]. |