V.5 No 2 |
1 |
| Supplement 2. The answers to Sergey Khartikov’s questions | |
|
|
V.5 No 2 |
1 |
| Supplement 2. The answers to Sergey Khartikov’s questions | |
|
|
Supplement 2. The answers to Sergey Khartikov’s questions After the publication of our paper on black holes and in parallel with that of Supplement 1, we discussed this subject with Mr Sergey Khartikov and answered in the Supplement 1 to a part of his questions. He expressed a doubt and asked new questions, though, as it will be seen, much transformed. Since at all events these questions concern the basic aspects of our paper and crucial points of understanding the black hole conception wrong, we decided to write the Supplement 2 as Mr Khartikov’s questions and our answers. To make this material more visual, we denoted our previous answers to Mr Krartikov on which he bases in olive colour, his new questions in bluish-green, citations from literature - in usual for our journal green colour, and the questions will be numbered in red. 1. Citation: “As to the reecord of metric transformation, here you are multiply incorrect”. Sergey, the formula (18) of your work
means the calculation of Jacobian of coordinate transformation in the plane Euclidean
space. In the Schwarzschild problem, the space is initially Riemann’s, so your
formula (18) wittingly never will match the Schwarzschild’s Jacobian. You derived
your (18) for the equation (16). Calculate the same for the initial equation (14) and you
will see, the results will differ strongly by the multiplier r2 sin I would repeat this result, to avoid any
vagueness: the root of determinant for the metric (14) multiplied by the Jacobian r2 sin Let us start from your point as if we determined the Jacobian in the plane Euclidean space and Schwarzschild – in that Riemann. In transition from the metric in rectilinear coordinates ((14) of our paper) |
| (1) |
to the metric in spherical coordinates ((16) of our paper) |
| (2) |
Schwarzschild used the standard transformation formulas namely for the plane Euclidean space ((15) of our paper) |
| (3) |
which you certainly could not omit, emphasising the previous and following formulas. In the Riemann space, the transformation (3) generally is not true. In the previous post to you, besides the cited above, we wrote also much, in particular to this point: “In your meaning it would be correct to write |
| (4) |
taking separately the metric tensor and coefficient Fik , though in this case it appears also necessary to account G and H. ;-)”. After this, we substantiated the necessity to account these coefficients in transformation. In this light, it would be interesting to recall our claim to (1) in (2) of our paper. “In accordance with the conventional mathematical formalism of tensor analysis, in this case of orthogonal metric |
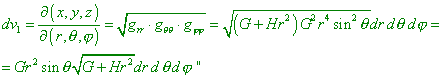 |
(5) |
[1, p. 6]. In (5) we see the Jacobian in most general form, which is used in transformations in curvilinear coordinates. Just on the basis of (5) we concluded incorrect the following Schwarzschild’s opinion: “With it the element of volume in spherical coordinates is equal to |
| (6) |
so that the Jacobian of transformation
from old coordinates to those new equal to r2 sin |
| (7) |
Schwarzschild already could not satisfy the equality |
| (8) |
as he had to satisfy another equality, |
| (9) |
[1, p. 6]. So your claims to our paper have no grounds in
this case. Not we but Schwarzschild transformed in the metric of Euclidean space. The same, the description of calculation of which you are
writing does not fit the mathematical operations that have to take place really in passing
from (1) to (2) with the following passing to (9). The point here is not that “the root of determinant of the metric (1) multiplied by the Jacobian
r2
sin |
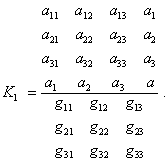 |
(10) |
To this invariant there have to be involved just the
coefficients H and G whose presence in our computations you claimed illegal.
|