SELF |
6 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
6 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
10. Citation: “If in a NRF, even in the local meaning, the light speed was constant, Einstein’s formula ( (4) of your work), as well as his ( (7) of your work) are senseless, as they were written namely in that first approximation”. Reply: These formulas have been written not for the light speed measured by the local observer. They have been written for the observer at some (any) point of space in relation to which the so-called ‘world time’ is read. SO there is no contradiction. First of all, analysing the item 6 of your reply, we got to see that Einstein’s formula has originated from the incorrectly joined results yielded in the IRF with the incorrect transformations in the NRF, in the ungrounded supposition as to the gravity affection on the light speed, with wholesale substitution of the non-uniform acceleration by that uniform and illegal application of SR to the NRFs. One of these defects is sufficient to disregard this Einstein’s derivation at all, even as a hypothesis; the more it is unworthy to state this derivation correct. The more, as we could make sure, Einstein’s formula was not written for the ‘world time’, as you are stating. It was written namely for the local observer. This was caused by the fact that in the denominator of Einstein’s expression |
| (39) |
there has to be not some abstract speed c and not the same value of speed which we see in the left part of (39) but the local value of the light speed at the moment of radiation, i.e. c0 . And the direct substitution of this value to (39) yet does not solve the problem. Actually, if we return to the analysis of the item 6 of your reply, to the expression (27), then, substituting to it the value of relativistic total energy (31), we yield |
| (40) |
or |
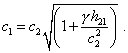 |
(41) |
This is a very complicated regularity that coincides with
that Einsteinian neither in strong nor in weak fields, nothing to say of correctness of
this regularity from the view of above analysis. In the right part of (41) you see not the
gravity potential but the product of the value of interval by |
| (42) |
Hence, |
| (43) |
where g2 is the free fall acceleration at the point of light radiation. With it, (41) will take the following form: |
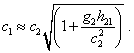 |
(44) |
In order (44) to become exact, we have to pass from the finite value h21 to the infinitesimal increments. We will yield |
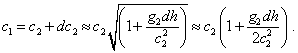 |
(45) |
It follows from (45) that |
| (46) |
To integrate (46), we have to account the dependence of g2 on the distance from the gravity field source, which is determined by (42). Noting this, we yield |
| (47) |
Or, omitting the indexes that became unnecessary and integrating, yield |
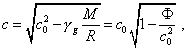 |
(48) |
where the gravity field potential is determined at the point of light speed variation, and c0 is determined at the infinitely distanced point. Then we may speak of some world time, although looking back to the whole chain of substitutions that we revealed in the item 6. We would mark, according to the formula, in approaching to the gravitating body the speed not increases but decreases; this is caused by Einstein’s confusion with the signs before the gravity potential and by the features of derivation of the initial expression. But even if we account this all, we will not yield the formulas with which Einstein operated, nothing to say that we may not agree with the conclusions of his work that described the light speed regularity with respect to the gravity potential. We just wrote of it in the item 2 of our paper. At this point we finish answering your post, supposing, you could get the answers to your secondary questions from the above analysis, as well as taking into account the results of study stated in our next paper, “On basic formalism of special theory of relativity”. Yours sincerely, Sergey and Olga Karavashkin
|
References: 1. Karavashkin, S.B. and Karavashkina, O.N. On reality of black holes. SELF Transactions, 5 (2005), 2, 1- 17 2. Schwarzschild, K. On the gravity field of point mass in Einsteinian theory. Sitzungsber. d. Berl. Akad., 1916, s. 189. Cited after Russian edition: Schwarzschild, K. On the gravity field of point mass in Einsteinian theory. - In: Albert Einstein and the theory of gravitation. Collection of papers, p. 199- 207. Mir, Moscow, 1979 (Russian) 3. Landau, L.D. and Lifshiz, E.M. Field theory. Nauka, Moscow, 1973 (Russian) 4. Einstein, A. On the general theory of relativity. - In: Collection of scientific works, vol. 1, p. 425. Nauka, Moscow, 1965 (Russian) 5. Einstein, A. The formal initials of the general theory of relativity. - In: Collection of scientific works, vol. 1, p. 326. Nauka, Moscow, 1965 (Russian) 6. Doroshkevitch, A.G., Zeldovvitch, Ya. B. And Novikov, I.D. The gravity collapse of asymmetric and rotating masses. - In: Albert Einstein and the theory of gravitation. Collection of papers, p. 396- 414. Mir, Moscow, 1979 (Russian) 7. Einstein, A. On the affection of gravity force on the light propagation. - In: Collection of scientific works, vol. 1, p. 165. Nauka, Moscow, 1965 (Russian) 8. Dyson, F.W., Eddington, A.S., Davidson, C. The determination of light beam deviation in the gravity field of Sun, after the data of observation during the full Sun eclipse on May, 29, 1919. Phil. Trans. Roy. Soc., ser. A, 220, 291 (1920). Cited after Russian edition: Dyson, F.W., Eddington, A.S., Davidson, C. The determination of light beam deviation in the gravity field of Sun, after the data of observation during the full Sun eclipse on May, 29, 1919. - In: Albert Einstein and the theory of gravitation. Collection of papers, p. 564- 570. Mir, Moscow, 1979 9. Penrose, R. Gravity collapse and space-time singularities. - In: Albert Einstein and the theory of gravitation. Collection of papers, p. 390- 395. Mir, Moscow, 1979 (Russian) 10. Vavilov, S.I. Experimental grounds of the theory of relativity (1928). - In: Collective works, vol. 4. P.H. of the Academy of Sciences of USSR, Moscow, 1956, p. 9- 110 (The reference 31 in: Atsukovsky, V.A. The critical analysis of the foundations of theory of relativity. Petite, 1996, Russian) 11. Sharonov, V.V. Refraction of light in the atmosphere. - In: Physical encyclopaedia, vol. 4, p. 443. Soviet encyclopedia, Moscow, 1964 (Russian) 12. Einstein, A. On the principle of relativity and its corollaries. - In: Collection of scientific works, vol. 1, p. 65. Nauka, Moscow, 1965 (Russian) |