V.5 No 2 |
5 |
| Supplement 2. The answers to Sergey Khartikov’s questions | |
|
|
V.5 No 2 |
5 |
| Supplement 2. The answers to Sergey Khartikov’s questions | |
|
|
None the less, basing on the same ungrounded equivalence principle, Einstein without substantiation, by a trick, introduced a quite specific regularity that determines the light - gravity field interaction in full analogy with interaction of material bodies with this field. While the basic difference in properties of light and material bodies is well known. In particular, at the point of material bodies interaction, they reflect from each other and re-distribute their speeds after reflection in accordance with the conservation law of the pulse of system. While the light rays pass through each other without any reflection either scattering, and this of course reflects on the conditions of light - gravity field interaction. Basically, having shown this substitution in Einstein’s statement of problem, we may stop analysing. And you are saying, his derivation is correct and clear… And we still did not reach the issue, whether the transition from IRF to NRF is correct. Well, meeting your wish to see precisely Einstein’s mistake in transition from IRF to NRF, let us go on with our analysis. When Einstein, basing on a half-determined statement of problem, without grounds has substituted the RF in the gravity field for the uniformly accelerated RF, he additionally determined the statement of problem. He specified the properties of RF K with reference to which the systems S1 and S2 were stationary. Now with respect to K0 the RFs S1 and S2 are moving with the uniform acceleration. “Suppose, we are discussing the process of radiation energy transfer from S2 to S1, being in the reference frame K0 , which is non-accelerated” [7, p. 168]. But this also is insufficient - to introduce the equivalence principle. As we showed in the page 15 of our paper, the inclined motion of body in the freely falling RF will warp the body’s trajectory. Similarly in the case of uniform motion of RF inclined to the direction of gravity force. If the gravity field affects the light, in this RF it will act under an angle to the RF ’s motion; this means, the body’s trajectory will be not the resultant of uniformly accelerated motion but of warped motion - and equivalence principle appears violated again. So we see, Einstein introduces not simply RF K0 but gives to it quite specific properties of stationary state or of uniform motion along the gravity force, and in this way he much limits the generalisation of problem. In its turn, it means that the changed conditions of ray’s motion violate the regularity which Einstein sought. Furthermore, let us draw our attention that the RF in which Einstein carries out his study is inertial, just as we pointed you before. While the RFs S1 and S2 are located in the accelerated frame K' , and the next Einstein’s step corroborates it. “Suppose, at the moment when the radiation energy E2 is transferred from S2 to S1, the frame K' has zero speed with respect to K0 . The rays will achieve the frame S2 in the time h / c (in the first approximation)” [7, p. 168]. Here we have to stop again, as there appeared the indefinite parameter of the light speed in the denominator. To sort this issue out, we will point, Einstein’s model is shown in Fig. 5.
|
|
Fig. 5. Einstein’s calculation diagram of the ray energy variation in propagation from S2 to S1
|
The property of this diagram is that the accelerated, as Einstein thought, motion of the ray in relation to the stationary and inertial RFs S1 and S2 has been substituted by the accelerated motion of these frames with respect to the uniformly propagating ray in the frame K0 . But if in this diagram both frames S1 and S2 propagate uniformly, we will not see any change of speed in relation to S1 and S2 , as the gravity field will equally accelerate all material bodies located in it, to which Einstein attributed also the light. Proceeding from this, the light energy will not change with respect to the frame K0 . And K' is not an IRF and we may not pass from K0 to K' in limits of SR. But as the next step Einstein does just so: “At this moment (when the rays achieve S1 - Authors) the frame S1 has with respect to K0 the speed |
| (26) |
So, according to the usual theory of relativity (SR - Authors), the radiation that achieved S1 has not the energy E2 but the larger energy E1 , which in the first approximation is connected with the energy E2 by the relationship |
| (27) |
[7, p. 168]. But besides in SR we may not pass from the IRF to NRF, the very law of energy transformation in SR is other: “the energy of (uniformly) moving frame unaffected by the outer forces is a function of two variables, namely: of the energy E0 of the frame in relation to the accompanying reference frame and of the speed of the frame’s shift q, and |
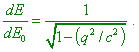 |
(28) |
It follows from this that |
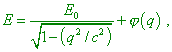 |
(29) |
where |
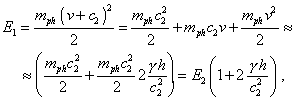 |
(30) |
where mph is the mass of photon. But then this operation does not mean the passing from IRF to NRF. And the solution in (30) differs from (27) by the doubled summand in the brackets. Should Einstein took the formula for complete energy as |
| (31) |
in accordance with (30) he would yield the same result. And several basic mistakes were added here. Firstly, if the light speed was variable, in passing from K0 to K' it has to be transformed in full accordance with the laws of relativistic mechanics. But if the very light speed is transformed, what have we to take as the invariant? The light speed at the moment of its radiation? No, we may not, as the light speed constancy does not make this value invariant. The light speed at the infinity? But in this local consideration it is irrelevant to the problem. The expression (26) was yielded exceptionally for the light speed at the moment of radiation, and we can easily show it. Actually, in accordance with Fig. 5, the time which the ray spends to pass the distance from S1 to S2 is |
| (32) |
While (32) has been written namely for K0 in which the light speed is constant, and noting that zero speed of S2 at the initial moment is determined by the light speed at the moment of radiation. On the other hand, the way which a ray has to pass until it was received by S1 is |
| (33) |
And this expression is also written for K0 . Substituting (32) to (33), we yield the quadratic equation |
| (34) |
The expression |
| (35) |
is the solution of this equation, noting the non-negative time intervals. In the weak fields with |
| (36) |
we yield |
| (37) |
which coincides with the Einstein’s expression, with the addition that the light speed is not an abstractly-arbitrary thing but is equal to that value at the moment when it was radiated by the system S2. From this we yield directly that the speed of S1 is equal to |
| (38) |
But we would repeat, this calculation was made in the IRF K0 . According to the relativistic conception, to make use of these solutions in K' , we have to pass to this RF. This is quite difficult, as the light speed already is not constant - at the radiation point it has one value and at the reception point, from the view of K' - another, and the light speed is inconstant by the statement of problem. Thus, Einstein might not make even the operation that was given by the derivation of (30), and of course he might not apply the transformation directly. And with it you are stating in your item 8: “The calculation was transferred to the NRF illegally (in limits of SR and GR, of course) - considerations are the same as in the item 6”. As you can see, neither Einstein nor you are right in this issue, and you cannot be right, as SR does not deal with NRFs, the more with inconstant speed of light given by the very statement of problem. And the locality condition will not help you – again, because of given light speed inconstancy. With this analysis we can think lifted some your questions and statements, items 7- 9, and may pass straight to your item 10. |