т.7 No 1 |
3 |
| О неоднозначности преобразований между инерциальными системами в СТО | |
|
|
т.7 No 1 |
3 |
| О неоднозначности преобразований между инерциальными системами в СТО | |
|
|
2.3. Взаимоотношение углов во взаимно движущихся системах отсчета с точки зрения релятивистской концепции При представлении решения задачи о преобразованиях координат путем введения промежуточных систем отсчета мы могли убедиться, что различные пути приводят к различным решениям, что не характерно для евклидовых пространств. В качестве одной из предполагаемых причин подобного несоответствия релятивисты обычно приводят искажение углов при преобразованиях или поворота осей на мнимый угол. Вместе с тем, как известно, одним из условий постановки Эйнштейном задачи нахождения преобразований Лоренца является именно параллельность координат: “Пусть теперь началу координат одной из этих систем (k) сообщается (постоянная) скорость v в направлении возрастающих значений x другой, покоящейся системы (K); эта скорость передается также координатным осям, а также соответствующим масштабам и часам. Тогда каждому моменту времени t покоящейся системы (K) соответствует определенное положение осей движущейся системы, и мы из соображений симметрии вправе допустить, что движение системы k может быть таким, что оси движущейся системы в момент t (через t всегда будет обозначаться время покоящейся системы) будут параллельны осям покоящейся системы” [1, с. 13]. На данной обусловленности взаимной параллельности осей Эйнштейн основывает исходные уравнения преобразований в общем виде, которые в ходе его вывода приобретают форму преобразований Лоренца: “… можно выбрать обе системы координат так, чтобы ось x системы S и ось x' системы S' совпадали и чтобы отнесенная к S ось y' системы S' была параллельна оси y системы S… Из известного теперь положения координатных плоскостей системы S' относительно S непосредственно вытекает, что каждые из следующих уравнений попарно эквивалентны: |
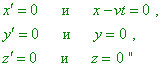 |
(16) |
[4, с. 71]. Как мы можем видеть из цитаты, система уравнений (16) записана именно для параллельности осей взаимно движущихся систем отсчета и никаких поворотов не предполагает, как не предполагает и преобразований в криволинейных пространствах. Также неосновательны ссылки релятивистов на повороты при преобразованиях. Подобные повороты в линейных пространствах задаются принципиально отличными от (16) выражениями, а пространство СТО по условию, введенному Эйнштейном, строго линейно: “Можно сразу сказать, что эти уравнения должны быть линейными по отношению к указанным переменным, поскольку этого требуют свойства однородности пространства и времени” [4, с. 71]. Из этой же линейности следует и то, что трехмерное пространство СТО (пространственные оси) является евклидовым: “Равенство нулю тензора кривизны в евклидовом пространстве очевидно. Однако уже Риман в своей диссертации указал, что верна и обратная теорема: если тензор кривизны равен нулю, то пространство – евклидово, т.е. тогда можно найти такую систему координат, в которой gik постоянны. Впервые обстоятельное доказательство этого утверждения дал Липшиц. Очень изящное и наглядное рассуждение было проведено Вейлем” [2, с. 78]. Таким образом ни о нелинейности пространства, ни о преднамеренных поворотах осей в теореме Эйнштейна говорить не приходится, а значит, в обоих вариантах, представленных в п. 2.2, все оси основных и вспомогательных систем отсчета сохраняют свою взаимную параллельность и в обоих случаях преобразование происходит из одной и той же системы отсчета S1 в ту же самую систему отсчета S2 . Тем не менее, чтобы снять излишние возражения релятивистов, рассмотрим закономерность преобразования углов во взаимно движущихся системах отсчета. При этом сразу обратим внимание на тот факт, что мы в данном случае не можем воспользоваться стандартной релятивистской формулой трансформации углов [2, с. 32]: |
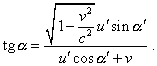 |
(17) |
В соответствии с обозначениями Паули, выражение (17) записано для преобразования угла наклона скорости при переходе из подвижной (штрихованной) системы отсчета в неподвижную (нештрихованную). Именно в связи с этим в правой части (17) фигурирует не только взаимная скорость систем отсчета v , но и скорость тела u' относительно подвижной системы отсчета. А это в релятивистском формализме означает, что для неподвижных относительно подвижной системы отсчета тел, с которыми обычно соотносят начало системы отсчета, формула (17) теряет смысл и для преобразования пространственных углов нужно использовать иную зависимость, выведенную именно для преобразования углов пространственного вектора, неподвижного относительно подвижной системы отсчета. Отметим здесь, что в классической физике данное различие абсурдно, но в рамках ее формализма не происходит и трансформации пространства-времени, как и сохраняется соответствие между углами наклона векторов во всех инерциальных системах отсчета. В релятивизме это условие преднамеренно нарушено, поэтому и закономерности трансформации углов необходимо искать для векторов скорости отдельно и для пространственных векторов отдельно, и как мы увидим дальше, данные зависимости принципиально различны. Чтобы найти закономерность
трансформации пространственных углов при
переходе из одной инерциальной системы отсчета в
другую в рамках релятивистской концепции,
рассмотрим две инерциальные системы отсчета K
и K' , из которых последняя движется в
направлении положительных значений оси x
системы отсчета K с сохранением полного
совпадения осей x и x' . Пусть также в
системе отсчета K' находится
пространственный вектор
|
Рис. 6. Схема движения
пространственного вектора
|
Чтобы корректно произвести расчет искомой зависимости углов, мы должны, в отличие от классического формализма, учитывать не только пространственные, но и временные характеристики, поскольку, как показано нами в предыдущих работах, преобразования Лоренца наклоняют плоскость событий, вследствие чего появляется мнимая неодновременность. И если мы предполагаем, что угол наклона пространственного вектора производится в физическом времени каждой системы отсчета (что соответствует условию вывода Эйнштейном преобразований Лоренца), то мы должны производить дополнительные преобразования, чтобы согласовать результаты преобразований с физическим временем в каждой системе отсчета. С учетом вышеописанного, чтобы
преобразовать вектор для начала вектора x'1 = 0 , y'1 = 0 , t' = t'0 и |
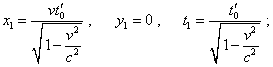 |
(18) |
для конца вектора x'2
= N' cos |
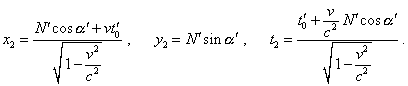 |
(19) |
Из (18) и (19) мы видим, что координаты начала и конца вектора в неподвижной системе отсчета, как и ожидалось, отображаются в различные моменты времени. Чтобы ввести в соответствие полученные значения с физическим временем в неподвижной системе отсчета, достаточно учесть, что все точки, соответствующие этому пространственному вектору, равномерно смещаются во времени вдоль оси x системы отсчета K . Поэтому если положение начала вектора (x1 , y1) соответствует времени t1 , то в этот момент времени конец вектора находился в точке с x-проекцией |
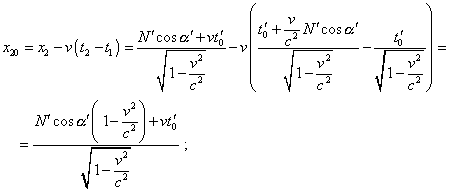 |
(20) |
y-проекция конца вектора при этом соответствует (19), поскольку смещение происходит вдоль оси x . С учетом (20) и (18), разность x-проекцией в неподвижной системе отсчета равна |
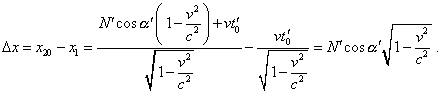 |
(21) |
Из (18) и (19) имеем для y-проекций |
| (22) |
Следовательно |
| (23) |
Полученное выражение (23) описывает искомую зависимость, связывающую углы наклона пространственного вектора во взаимно движущихся инерциальных системах отсчета в релятивистской концепции. Сравнивая это выражение с законом трансформации векторов скорости (17), мы видим принципиальное отличие в самом характере зависимости. Это свидетельствует о том, что вектора различной природы в релятивистской концепции преобразуются различным образом. Далее, из (23) мы видим, что углы
наклона пространственных векторов, направленных
вдоль осей подвижной системы отсчета, не
трансформируются, т.е. при 2.4. Доказательство сохранения параллельности осей при переходе из неподвижной системы отсчета в подвижную с использованием промежуточной системы отсчета, движущейся в направлении одной из проекций В предыдущей задаче мы рассмотрели закономерности трансформации наклонного пространственного вектора, движущегося с началом подвижной системы отсчета, и показали, что при горизонтальном и вертикальном положении этого вектора трансформация угла наклона отсутствует. В данной задаче мы усложним движение этого пространственного вектора, заставим его смещаться еще и в поперечном направлении. Пусть имеются неподвижная инерциальная система отсчета S1 и подвижная система отсчета S' , движущаяся по оси x1 неподвижной системы отсчета со скоростью vx1 в направлении положительных значений x1 , сохраняя параллельность осей. И пусть имеется некоторый отрезок AB , движущийся вместе с системой отсчета S' и одновременно с этим в направлении оси y' . При этом движение осуществляется таким образом, что точка A отрезка движется строго по оси y' , как показано на рис. 7.
|
Рис. 7. Схема движения отрезка AB относительно систем отсчета S1 и S'
|
Положим, что длина отрезка
равна l , продольная скорость отрезка как
целого с точки зрения неподвижной системы
отсчета равна vx1 , поперечная скорость,
опять-таки с точки зрения неподвижной системы
отсчета равна vy1 , а угол наклона отрезка к оси x1
равен Для решения поставленной задачи прежде всего запишем уравнения движения исследуемого отрезка в неподвижной системе отсчета S1 . Для этого нам достаточно записать уравнения движения его начала и конца. С учетом начальных условий, данные уравнения будут иметь вид |
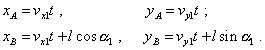 |
(24) |
Следующим шагом определим законы движения концов стержня в подвижной системе отсчета. Для этого, как и в предыдущей задаче, нам необходимо доопределить задачу и учесть фактор физического времени. Чтобы сделать это корректно, вспомним, в связи с чем появилась задача о стержне при рассмотрении основной задачи о переходе из системы отсчета S1 в систему отсчета S2 , движущейся плоскопараллельно относительно S1 под углом к ней. Эта задача возникла в связи с тем, что нам необходимо доказать, что при использовании промежуточных систем отсчета S' и S" , движущихся в направлениях проекций скорости движения системы отсчета S2 , оси S2 не поворачиваются относительно S1 . При этом, поскольку в основной задаче рассматривается переход между S1 и S2 , то ориентация осей S2 в физическом времени S' не играет никакой роли. Важен вопрос, поворачивается ли S2 по отношению к S1 при переходе через S' или S" . Исходя из этого, а также учитывая, что в преобразованиях Лоренца закладывается, как правило, физическое время той системы отсчета, из которой мы осуществляем преобразования, т.е. в данном случае S1 , нас интересует сохранение параллельности осей S2 именно по отношению к S1 , в физическом времени исходной системы отсчета S1 . Стержень же мы можем рассматривать как некоторую обобщенную модель осей системы отсчета S2 . Определившись в данном вопросе, мы можем продолжить исследование. Исходя из дополнительного условия, а также учитывая, что подвижная система отсчета движется в направлении оси x1 , будучи параллельной ей, мы можем записать уравнения движения концов стержня в подвижной системе отсчета в виде |
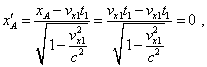 |
(25) |
| (26) |
Из полученных выражений мы видим, что конец A стержня в подвижной системе отсчета движется строго вертикально. Преобразование для времени мы не производим, поскольку нас интересует трансформация угла наклона стержня в физическом времени системы отсчета S1 . Для конца B имеем |
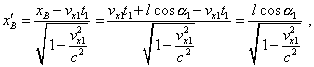 |
(27) |
| (28) |
Из (27) мы видим, что второй конец стержня также движется строго вертикально, поскольку x' не зависит от времени. Вместе с тем в системе отсчета S' и время входит только в y' -проекции. Но и оно сокращается вследствие того, что для определения угла наклона стержня в подвижной системе отсчета нас интересуют не абсолютные значения проекций, а разности значений между положением концов стержня в каждый момент времени. Поэтому |
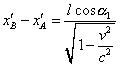 |
(29) |
и |
| (30) |
С учетом (29) и (30) у нас отпадает необходимость вычисления преобразования времени. Одновременность же с точки зрения системы S1 мы фактически учли в ходе подстановки (26) и (28) в (30). Используя (29) и (30), мы можем определить угол наклона стержня относительно подвижной системы отсчета S' в физическом времени системы S1 . И этот наклон стержня, как уже было сказано, при определенной ориентации будет моделировать положение осей S2 по отношению к S1 : |
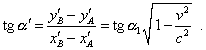 |
(31) |
Из (31) следует, что положение
направленного отрезка AB , имитирующего оси
системы отсчета S2 при ориентации, кратной k Также из проведенного исследования следует, что неоднозначность, возникающая при различных переходах из S1 в S2 , не связана с тем, что в зависимости от пути мы приходим в различные системы отсчета. Мы видели, что идя через промежуточные системы S' или S" , движущиеся в направлении проекций скорости, мы не изменяем наклон системы отсчета S2 по отношению к S1 , а используя в обоих случаях одну и ту же физическую точку A2 для построения S2 , мы в обоих случаях приходим к системе отсчета, в начале которой расположена одна и та же физическая точка A2 , а оси в обоих случаях сохраняют параллельность системе отсчета S1 . Неоднозначность полностью обусловлена неоднозначностью результата, который получается при использовании преобразований Лоренца. И это важный вывод, показывающий, что причина различия, возникшего между первым и вторым вариантами в п. 2.2, не обусловлена тем, что идя различными путями, мы якобы приходим к различным системам отсчета S2 . Выкладки показывают, что если мы при произвольном числе промежуточных систем отсчета будем переходить от одной системы отсчета к другой, используя движение последующих промежуточных систем отсчета вдоль осей предыдущих систем отсчета, то независимо от количества этих промежуточных систем, параллельность осей всех систем отсчета будет сохраняться. А следовательно, идя различными путями от исходной системы отсчета S1 к конечной системе отсчета S2 через посредство промежуточных систем, двигающихся в направлении осей исходной системы S1 , мы будем всегда получать систему отсчета S2 той же ориентации, но различной степени продольной трансформации длин по осям, свидетельствующей исключительно о неоднозначности перехода, осуществляемого преобразованиями Лоренца при произвольном инерциальном движении систем отсчета. |
Содержание: / 1 / 2 / 3 / 4 /