СЕЛФ |
4 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
СЕЛФ |
4 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
3. Задача о преобразовании координат между произвольно движущимися в плоскости инерциальными системами отсчета с точки зрения классического формализма В данном пункте мы для сравнения с формулами преобразования, полученными в п. 2, определим уравнения преобразования из неподвижной системы отсчета в подвижную в рамках классического формализма. При этом мы будем использовать те же самые схемы. 1 ВАРИАНТ решения задачи Для начала определим уравнения, используя промежуточную систему отсчета S' , движущуюся относительно S1 в направлении положительных значений x1 со скоростью vx1 . Учитывая построения на рис. 2, формулы перехода между S1 и S' в классическом формализме имеют вид |
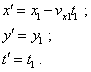 |
(32) |
Соответственно формулы перехода из S' в S2 будут иметь вид |
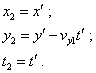 |
(33) |
Объединяя (32) и (33), получим |
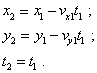 |
(34) |
2 ВАРИАНТ решения задачи Теперь решим задачу, используя промежуточную систему отсчета S", которая будет двигаться в положительном направлении оси y1 со скоростью vy1 . В соответствии с построением на рис. 4, формулы перехода из S1 в S" будут иметь вид |
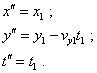 |
(35) |
Соответственно формулы перехода между S" и S2 будут иметь вид |
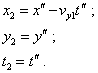 |
(36) |
Подставляя (35) в (36), получим |
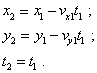 |
(37) |
Сравнивая (34) с (37), мы можем убедиться, что формулы преобразования в классической физике не зависят от пути, по которому они были получены, что находится в полном соответствии с условием однородности и изотропности пространства, для которого они были выведены. 4. Об однозначности отображения как объективной необходимости качественного описания процессов в природе В предыдущих пунктах работы мы на основе двух феноменологических подходов к описанию природных явлений получили полностью противоположные результаты. С точки зрения классической физики, каким бы образом мы ни осуществляли переход между двумя инерциальными системами отсчета, мы получаем одну и ту же зависимость, с помощью которой осуществляем связь параметров взаимно движущихся систем отсчета. С точки зрения релятивистского формализма это далеко не очевидно, поскольку преобразования Лоренца приводят к различным результатам и тем самым зависят от пути, которым мы вели преобразование. Выявленное различие принципиально и поднимает вопрос о правомерности неоднозначности перехода между инерциальными системами отсчета при описании физических процессов. Если подобная неоднозначность допустима, то эйнштейновская ТО в данном смысле имеет право называться физической концепцией. Если же неоднозначность недопустима, то независимо от других факторов, данная концепция не может считаться физической теорией. Чтобы разобраться в данном вопросе, прежде всего определимся со стандартными свойствами, которые приписываются в физике однородному и изотропному пространству и времени. “В механической системе, достаточно удаленной от всех других тел, движение происходит совершенно одинаково, куда бы ее ни поместили. Это означает следующее. Пусть имеются две одинаковые механические системы с одинаковыми начальными условиями движения. Обе они весьма удалены от всех остальных тел, могущих действовать на них. Тогда, если рассматривать их в одной и той же системе отсчета, движение в них будет происходить строго одинаковым образом. Иными словами, движение не изменяется при переносе всех движущихся тел на одно и то же расстояние по взаимно параллельным отрезкам в один и тот же момент времени. Это утверждение основано, разумеется, на очень большом опытном материале, накопленном механикой за всю историю ее развития. В более краткой форме его принято называть свойством однородности пространства. Две равноценные механические системы, подобные описанным здесь, можно выбрать не только совмещенными, но и повернутыми относительно друг друга на любой угол. Опять-таки, если данные две системы достаточно удалены от всех тел, могущих действовать на них, движение в этих системах происходит одинаковым образом. Иначе говоря, все направления в пространстве равноценны. Это свойство пространства называется еще изотропией. Изотропия пространства так же является обобщением опыта, как и его однородность” [5, с. 19]. С изотропией пространства непосредственно связано выполнение законов сохранения энергии и импульса в динамике: “…законы сохранения были получены как следствие уравнений движения Ньютона. Поэтому они связаны со свойствами пространства и времени, которые постулируются в классической механике” [6, с. 102]. В приведенных определениях изотропии и однородности пространства молчаливо признается за очевидное, что отображение положения тел и их траекторий в каждой системе отсчета должно быть однозначным. Доказывается же это в рамках высшей геометрии: “Если векторы e1 и e2 , имеющие общее начало O и неколлинеарные между собой, фиксированы, то любой радиус-вектор r допускает разложение |
| (38) |
где числа x1 и x2 определяются единственным образом. Обратно, по заданной паре чисел x1 , x2 и векторам e1, e2 строится единственный радиус–вектор |
Пара векторов e1, e2, имеющих общее начало и неколлинеарных между собой, называется базисом. Система чисел x1 , x2 , которая участвует в разложении |
произвольного радиус–вектора r по элементам базиса e1, e2, называется аффинными координатами вектора r ” [7, с. 100]. В свете указанной теоремы однозначности отображения в линейном базисе, понятно, что положение любой материальной точки, как и их совокупностей, должно быть однозначно определено в выбранном базисе. Теперь с учетом этого представим, что в некотором пространстве движется инерциально материальная точка и за ней наблюдают два наблюдателя, находящихся в началах своих инерциальных систем отсчета, из которых S2 движется относительно S1 с некоторой скоростью v , вектор которой не совпадает с направлением движения тела, как показано на рис. 8.
|
Рис. 8. Схема движения тела B относительно инерциальных систем отсчета S1 и S2
|
При представленной схеме движения тела B нахождение скоростей движения тела относительно систем отсчета S1 и S2 с точки зрения классического формализма не представляет никаких трудностей. Действительно, согласно полученным нами выражениям для перехода между системами отсчета S1 и S2 (34) и (37), имеем |
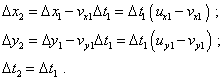 |
(39) |
Из (39) непосредственно получаем независимо от пути, по которому мы искали уравнения преобразований, |
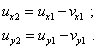 |
(40) |
При этом несложно видеть, что выражение (40) отражает правило параллелограмма, согласно которому сложение векторов определяется через сложение их проекций. В свете описанного интересно посмотреть, к чему приведет подобная операция для релятивистских уравнений преобразования. В этом случае мы уже не можем ограничиться одним выводом, поскольку в зависимости от направления перехода из S1 в S2 мы получили различные формулы (6)–(8) и (13)–(15) соответственно. Определим сначала проекции вектора движения тела B при преобразованиях (6)–(8). На основании (6) для х-проекции для смещения тела B имеем |
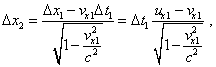 |
(41) |
для у-проекции на основании (7) имеем |
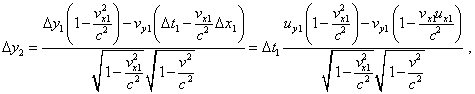 |
(42) |
наконец, на основании (8) для t-проекции получим |
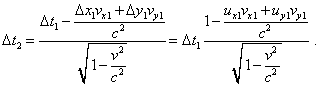 |
(43) |
Из (41)–(43) следует: |
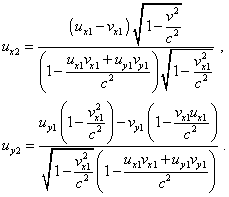 |
(44) |
Система (44) описывает проекции скорости тела в подвижной системе отсчета в рамках релятивистского формализма. Прежде всего, сравнивая (44) со стандартным выражением релятивистского суммирования скоростей (2), мы видим, что выражение (44) сводится к (2) при условии |
| (45) |
Это с одной стороны показывает правильность проделанных нами выкладок, а с другой стороны свидетельствует о том, что (44) является обобщением известного выражения сложения скоростей. Теперь рассмотрим второй вариант решения релятивистской задачи, основанный на решениях (13) – (15). На основании (13) для х-проекции для смещения тела B имеем |
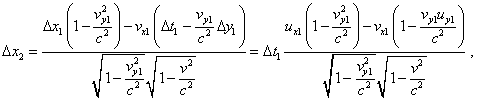 |
(46) |
для у-проекции на основании (14) имеем |
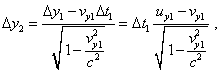 |
(47) |
для t-проекции получаем выражение, полностью аналогичное (43), поскольку в обоих вариантах время трансформируется одинаково. Теперь на основании (43), (46), (47) получим |
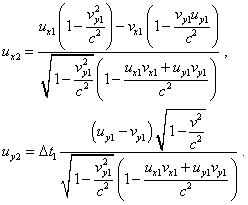 |
(48) |
Выражение (48) представляет второй вариант решения релятивистской задачи, принципиально отличающийся от (44). При этом характерно, что при выполнении условия (45), определяющего движение подвижной системы отсчета вдоль оси x , оба решения сводятся к (2). Это свидетельствует о том, что при одномерном движении системы отсчета раздвоения решения не происходит. Это раздвоение является следствием многомерного взаимного движения систем отсчета и обусловлено некоммутативностью преобразований в релятивистском формализме. Таким образом мы видим, что неоднозначность преобразования приводит к противоречию с базовой теоремой единственности разложения векторов в изотропном однородном пространстве и здесь затрагиваются не только свойства изотропного пространства, но и проявляются недостаточно полные законы описания матричных преобразований в приложении к описанию преобразований между системами отсчета. Действительно, когда описываются свойства алгебраического кольца, то как правило, его свойствам придают максимальную общность. Исходя же из этой общности “произведение двух матриц, вообще говоря, зависит от порядка сомножителей даже и в том случае, когда кольцо K коммутативно” [8, с. 13]. Как мы могли видеть из проведенного анализа, в случае применения матричного анализа к задачам, связанным с преобразованием координатных систем, на общие свойства матриц налагается условие однозначности отображения, которое дополняет общие требования к алгебраическому кольцу. При этом в случае преобразования Галилея никаких проблем не возникает, поскольку оно удовлетворяет как общим свойствам кольца, так и дополнительному условию. Действительно, полученные нами в п. 3 выражения последовательных преобразований можно записать в матричном виде следующим образом. При переходе в систему отсчета, движущуюся в направлении оси x , матрица преобразования будет иметь вид |
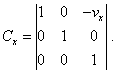 |
(49) |
При переходе в систему отсчета, движущуюся в направлении оси y , матрица преобразования будет иметь вид |
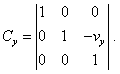 |
(50) |
Производя умножение матриц, несложно убедиться, что |
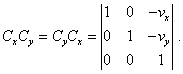 |
(51) |
При этом вид матриц настолько уникален, что малейшие изменения в любой из матриц в (49) или (50) приводят к некоммутативности результата. Вместе с тем, от того, как будет сохраняться закон преобразования между системами отсчета вне зависимости от пути, по которому мы будем переходить из одной инерциальной системы отсчета в другую, зависит не только формальный математический итог операции. От этого зависит и философское понятие познаваемости нами окружающих природных явлений. И это легко понять на простом примере. Предположим, что наблюдатель, расположенный в начале неподвижной системы отсчета S1 , не может непосредственно наблюдать за движением некоторого тела B , но имеет в распоряжении некоторые промежуточные станции, которые наблюдают это тело и движутся относительно неподвижного наблюдателя со скоростями v' и v" , как показано на рис. 9.
|
Рис. 9. Схема косвенного наблюдения за движением тела B
|
Если результаты наблюдения будут зависеть от того, каким путем они были получены, то нарушается детерминированность процесса исследования, и мы в качестве характеристики движения тела B можем принять любое произвольное значение в зависимости от того, какой промежуточной системой отсчета мы воспользуемся для наблюдений. Тем самым лишается какого-либо смысла и само наблюдение, поскольку достоверность его будет равна нулю. Таким образом, нарушение коммутативности преобразований автоматически приводит к нарушению базовой теоремы единственности разложения вектора в аффинном базисе, что приводит к запрету использовать данные разложения в формализме, опирающемся на некоммутативность преобразований из одной координатной системы отсчета в другую. Именно вследствие нарушения указанной базовой теоремы раздвоение отсутствует в случае одномерного движения подвижной системы отсчета. Но как только движение становится многомерным, немедленно проявляется противоречивость основы релятивистского формализма. Из этого вытекает, что само разложение как пространственных векторов, так и векторов скорости в релятивистском формализме некорректно. И это видно из представленного примера на рис. 9. Ведь и для промежуточной системы отсчета мы получим ту же самую неоднозначность, используя в свою очередь дополнительные промежуточные системы отсчета. При этом получится, что при измерении через промежуточные системы мы будем получать одни результаты, а при прямом измерении – другие, и это как было сказано нарушает детерминизм нашего наблюдения за процессами, протекающими в природе, что не подтверждается практикой. Выводы В ходе проведенного исследования было установлено, что преобразования Лоренца приводят к неоднозначности отображения вследствие нарушения базовой теоремы о единственности разложения вектора по ортам аффинного базиса, что лишает правомерности использовать разложения векторов в релятивистской концепции. Тем самым эйнштейновская концепция относительности входит в противоречия с законами отображения процессов в природе, и вследствие этого лишается права называться физической концепцией. Также показано, что единственной системой преобразований, удовлетворяющей принципу детерминированности описания физических процессов, являются галилеевы преобразования. Все другие типы преобразований координатных систем, кроме удовлетворения своей постулативной базе, обязаны проверяться на соответствие теореме единственности разложения векторов в аффинном базисе. В случае, если указанные преобразования не будут удовлетворять данному требованию, они не имеют права использоваться даже в качестве гипотезы. И этот тот самый критерий, который позволяет выявить соответствие концепции требованиям однозначности описания природных явлений. Литература: 1. Эйнштейн А. К электродинамике движущихся тел. Собрание научных трудов, т. 1, с. 7–35. Москва, Наука, 1965, 700 с. 2. Паули В. Теория относительности. Москва – Ленинград, Гостехиздат, 1947, 300 с. 3. Эйнштейн А. Принцип относительности и его следствия в современной физике. Собрание научных трудов, т. 1, с. 138–164. Москва, Наука, 1965, 700 с. 4. Эйнштейн А. О принципе относительности и его следствиях. Собрание научных трудов, т. 1, с. 65–114. Москва, Наука, 1965, 700 с. 5. Компанеец А.С. Курс теоретической физики, т. 1. Москва, Просвещение, 1972, 512 с. 6. Ольховский И.И. Курс теоретической механики для физиков. Москва, Наука, 1970, 447 с. 7. Бакельман И.Я. Высшая геометрия. Москва, Просвещение, 1967, 367 с. 8. Мальцев А.И. Основы линейной алгебры. Москва, Наука, 1970, 400 с. |
Содержание: / 1 / 2 / 3 / 4 /