94

S.B. Karavashkin, O.N. Karavashkina

We can see in Fig. 7 that actually in the line the standing waves produce, they are parallel to the excitation force direction. This last is easy explainable by the theorem and (22)-(26):

.

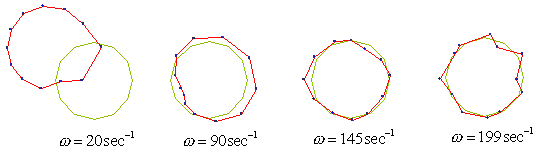
The construction in Fig. 8 corroborates it. It is clearly seen that with the varying external force inclination, the inclination of vibrations varies, too.

Furthermore, we can see from Fig. 7 that as the frequency tends to critical, the vibration shape tends to that antiphase, and according to (23)-(24), it remains such in the aperiodical regime. The only, in the aperiodical regime there is added the along-the-line damping which localises the external excitation energy in the external force action region.

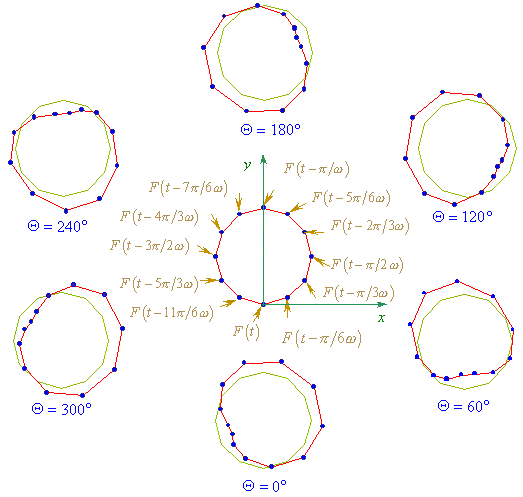
Fig. 9. The closed-loop homogeneous elastic line vibrations under the external distributed harmonic force acting as the travelling wave with the circular frequency = 90 sec^-1 and at the angle = 60^o, with respect to the external force momentary phase . The line parameters: n = 12; a = 0,02  m; s = 100 N/m; m = 0,01 kg; F₀ = 1 N; ₀ = 200 sec^-1

Basing on (21)-(22), we can easy obtain the solution for the case when a distributed force with the phase delay 2/n acts on a closed-loop line. This problem is applicable to the rotary and rolling models. To solve it, it is sufficient to sum the related solutions (21)-(22) in all elements, taking into account the delay of phases. The typical form of vibrations in such model is presented in Fig. 9. We see that unlike the above case, the travelling waves produce in the line, and the vibration pattern does not correspond to Fig. 7b. As opposite to the vibration pattern being formed in the line by a concentrated force, in this case the half-period wave process propagates in the line. And its propagation velocity is determined by the parameters of external force, not of the elastic line. With the growing frequency the vibration pattern complicates, but even when approaching to the critical frequency, the vibration pattern will not be so clearly expressed as in case of concentrated force action. We can see it well in Fig. 10, where the diagrams are presented dependently on the external force frequency.

Fig. 10. The closed-loop homogeneous elastic line vibrations under the external distributed harmonic force acting as the travelling wave at the angle = 60^o and at the moment = 0 , with respect to the external force circular frequency . The line parameters: n = 12; a = 0,02  m; s = 100 N/m; m = 0,01 kg; F₀ = 0,5 N; ₀ = 200 sec^-1

Thus, on the closed-loop elastic line model we see also that despite the bend angle does not effect on the solution directly, each specific model reveals its distinctions. But they are caused by the distinctions of transition between the reference systems.