Bend effect on vibration pattern098

SELF	98
S.B. Karavashkin, O.N. Karavashkina

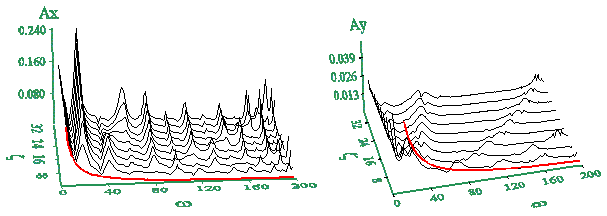
. Fig. 12. The amplitude-frequency characteristic for the longitudinal (a) and transverse (b) components of vibrations in an elastic line having the bend angle = 60^{^o} , with respect to the ratio of the transverse and longitudinal stiffness coefficients. The model parameters: m = 0,01 kg , F₀ = 1 N , k = 15, s_lt = 100 N/m , = 1,0 - 37,0 , = 60^{^o}
In Fig. 12 we see the amplitude-frequency characteristic of the longitudinal and transverse components of the wave in an elastic line before the bend, with respect to . At = 1 (the nearest curve in the plot) the amplitude-frequency characteristic has a hyperbolic form usual for ideal lines. With growing the resonance peaks arise in the plots; their amplitude grows with growing which can cause the local destructions on the quite stable general background. Some peaks in the middle band arise only at large values ; with growing the amplitude of some peaks first grows, then smoothes. The peaks of transverse component become shifted with growing . This is caused by growing _tr in accordance with (32). It is typical that despite the ideal pattern of elastic constraints, the amplitudes of resonance peaks are finite. The peak locations for the longitudinal and transverse components do not coincide too. In this connection, in such lines dependently on frequency either longitudinal or transverse vibrations can prevail. Thus, in the propagation of a wave having complex and especially continuous spectrum typical for solitary seismic waves, the essential transformation of the wave shape takes place. A number of frequencies are quenched in the wave travelling, and at the number of frequencies corresponding to the resonance peaks the vibration amplitude abruptly increases; this process is not synchronous for the longitudinal and transverse components. The smearing of the wave packet caused by dependence of the phase delay (of the propagation velocity in that number) on frequency adds to this. And taking into account that in the before-bend region a complex superposition of standing and progressive waves takes place, the velocity dispersion nonlinearly depends on the external excitation frequency.
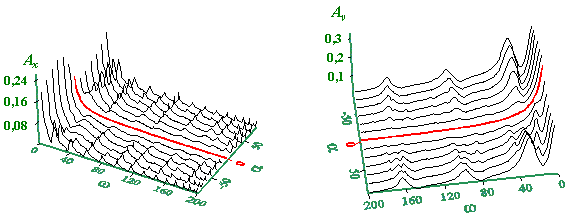
a b Fig. 13. The amplitude-frequency characteristic of the longitudinal (a) and transverse (b) components of vibrations in a line having different longitudinal and transverse stiffness coefficients with respect to the bend angle . The model parameters: m = 0,01 kg , F₀ = 1 N , k = 15, s_lt = 100 N/m , = 10 , = 45^{^o}
For the amplitude-frequency characteristic with respect to the bend angle of an elastic line, we see the similar pattern whose plots for the longitudinal and transverse components in the before-bend region are shown in Fig. 13. With = 0 (the red curve in the middle part of the diagram) the amplitude-frequency characteristic has a standard for an ideal line hyperbolic form even with > 1. With growing on the amplitude-frequency characteristic, there arise the resonance peaks whose amplitude increases with the growing , and their pattern depends not only on the value but also on the sign of . As applied to the seismic processes, it means that the abrupter transition from the flat country to the mountains is, and the abrupter the curvature of a mountain arc is (the Pamir knot is a typical example), the more destructive the earthquake consequences are. The same as in Fig. 12, the velocity of amplitude growing is different for different peaks. Some peaks reveal only at large values , with growing the low-frequency peak in Fig. 13 b coalesces with the next resonance peak, and the peaks location on the amplitude-frequency characteristic of the longitudinal and transverse components does not coincide.