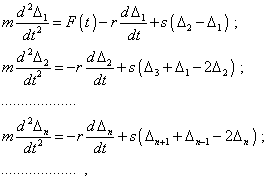SELF

18

S.B. Karavashkin and O.N. Karavashkina

Second, the solutions that one can yield by a conventional method are quite incomplete. As [10]–[13] show, the conventional methods do not enable us to study vibrations in the overcritical domain (over the boundary frequency 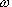₀). ''Solution of the boundary problems of vibration theory is basically reduced to determine the eigenvalues determination connected with the natural frequencies or other parameters of the studied system and to finding the eigenfunctions (vibration forms). If the eigenvalues and eigenfunctions have been found, we can think the boundary problem solved... At present a great number of approximate methods has been developed for finding the eigenvalues, but they all are quite laborious, give only the first eigenvalues, and the main, do not unite the study of systems with discrete and continuous mass distribution'' [5, p. 3- 4]. Only in some particular cases we have the incomplete, limitedly applicable solutions or mentionings that processes in the overcritical domain are possible (see, e.g., [7, p. 282–285], [8, p. 294], [14, p. 109]). At the same time, it is inherent in the vibration process in this domain that at the frequencies higher than critical, even an ideal elastic line behaves as a natural damper with along-the-line damping vibration amplitude. As we will show in this paper, the resistance essentially effects on the damping characteristics, as well as on the vibration pattern of the system elements. To make the analysis complete and high-quality, it is important to take into account, how the resistance effects on the elastic system vibrations. In our present study we will intentionally confine ourselves to a simple model of a semi-infinite 1D elastic line, to visualise the analysed processes. We will suppose that for other types of elastic lines we can obtain the alike results, since now we have available such exact analytical solutions as have been presented in [10]–[13].

2. Exact analytical solutions for a semi-infinite 1D elastic resistant lumped line

Seeking the exact analytical solutions for a studied elastic line, we will choose not a conventional way to find the particular solutions for a modelling system of differential equations. We will try to reduce the problem to the solutions for an ideal line presented in [10], the more it will be simple.

In our case the modelling system of differential equations will be

  is the external force and its amplitude, m is the mass of elastic line elements, and r is the mechanical resistance of constraints. Here and further n = 1, 2, 3, ..., and s will mean the stiffness coefficient of a line.