SELF |
32 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
32 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
Finally, ''Fisher has rigorously solved the sound propagation problem in an 1D chain of interacting particles, considering a disordered chain of particles located along the axis x '' [16, p. 90]. Fisher has found his model on the state equation, basing it on the potential of forces acting between a pair of particles |
| (44) |
where l is the average distance between a pair of nearest particles and T is the absolute temperature, and on the enthalpy equation |
| (45) |
Here k is Boltzman constant, and |
| (46) |
With it he has yielded an expression for the sound velocity squared as |
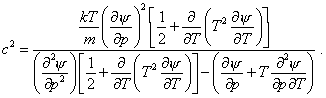 |
(47) |
“In the most general sense the
expressions (46) and (47) solve with absolute accuracy the problem of the sound velocity
calculation in an 1D liquid as a function of temperature and pressure at the given
potential At the same time, no one of mentioned theories takes into account the following factors studied in our work: the nonlinear affection of resistance on the parameters of vibration process and the features of vibration processes at the overcritical band. But if we compare the experimental data in Fig. 7 with the results presented in Fig. 3, we can easily see that the characteristics are comparable. And some below typical features enable this comparison. First of all, we see in Fig. 7 that in the low-pressure domain the anomalous dispersion of velocity takes place, increasing as approaching to the critical regime (the point of minimal value of the velocity), the same as in Fig. 3. The curves inclination after the extreme point also is approximately equal. Second, taking as the basic model a chain of the
elastically connected molecules, we may suppose that the increasing constraint stiffness
is related to the growing pressure at constant temperature. With it, one and the same
external excitation frequency corresponds to a more high-frequency band in Fig. 3, due to
the diminishing boundary frequency Third, it is known that the medium temperature increasing
at constant pressure can be achieved only if diminishing the medium density. This will
cause the increase of intermolecular distance a and fall of the constraint
stiffness s. In its turn, according to (15), it causes the growth of boundary
frequency and phase velocity in accordance with (27). Thus, the temperature growth will
shift the boundary frequency And the last, with growing temperature, the elastic system resistance will naturally increase. Summing up the above key points, we can explain qualitatively the curves behaviour in Fig. 7, using the regularities of the plot in Fig. 3. Each of dependencies c(p) in Fig. 7 has its distinctive minimum at the boundary
frequency From the presented brief qualitative analysis we can see that if taking into consideration the effect of resistance on the line vibration processes, we can essentially improve the conventional models and promote them to be better corresponding to the experimental data. |
Contents: / 17 / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 / 29 / 30 / 31 / 32 / 33 / 34 /