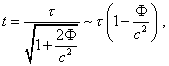т. 3 No 1

3

Заметки о физическом Абсолюте

Аналогичный вывод несложно сделать и в отношении других опытов релятивистов, в том числе и мысленных экспериментов. Взять хотя бы известный эйнштейновский парадокс часов. Этот мысленный эксперимент многократно обсуждался в литературе самого различного научного уровня. Достаточно полная библиография и описание всех возражений, связанных с этим парадоксом, приведены в работе [13]. При всех попытках убедить себя и окружающих в отсутствии парадокса, убедительного доказательства релятивистами так и не было представлено. Если стоять строго на позиции Маха, то по окончании ускорения космического корабля, инерциальные системы близнецов должны вновь становиться полностью идентичными и замедление времени должно быть чисто фиктивным и зависящим от используемой методики сверки часов. Действительно, если пользоваться излюбленной методикой релятивистов сверки часов путём фиксации интервалов, проходимых светом в сверяемых системах отсчёта, то различие будет иметь место, что следует и из галилеевого преобразования. Но не следует забывать, что в парадоксе близнецов вопрос стоит не об одновременности событий, а только о скорости течения времени. Поэтому, исходя из условия равноценности систем отсчёта, введенного самим Эйнштейном -

"Принцип относительности требует, чтобы полное совпадение законов распространялось также на случай, когда S ' движется равномерно и прямолинейно относительно S . В частности, скорость света в пустоте по отношению к обеим системам отсчёта должна выражаться одним и тем же числом" [Эйнштейн: 14, п. 3, с. 70- 71],

- мы можем, не выходя за рамки самой СТО, построить методику строгой синхронизации течения времени. Для этого достаточно воспользоваться фактом, что, согласно тому же Эйнштейну, формулы преобразования между системами отсчёта обладают определённой обратимостью; она выражается в том, что если мы имеем стандартную систему преобразований между двигающейся (штрихованной) системой отсчёта и неподвижной (нештрихованной) системой отсчёта, то,

"разрешая соотношения относительно x, y, z, t, нетрудно получить соотношения, отличающиеся только тем, что в них "штрихованные" величины заменены одноименными "нештрихованными" и наоборот, а вместо v стоит -v . Это следует непосредственно из того, что система S движется равномерно относительно S ' в направлении x' со скоростью -v" [14, п. 3 с. 73].

Поэтому, пользуясь расчётами самого Эйнштейна, мы можем заключить, что если у обоих близнецов имеются некоторые часы, идущие с частотой  f₀, то для каждого близнеца частота часов его брата будет определяться равенством

"… другими словами, часы, движущиеся относительно некоторой системы отсчёта со скоростью v, идут в этой системе медленнее в отношении  [1 - (v²/c²)] ^-1/2, чем те же часы в случае, если они покоятся относительно той же системы отсчёта" [14, п. 4, с. 74].

Таким образом, разница частот будет равна

и, учитывая написанное выше, данная разница в рамках СТО должна фиксироваться одинаково обоими братьями. Следовательно, если оба близнеца будут поддерживать равной полученную разность частот (6) и значение частоты собственных часов, регулярно сообщая друг другу значения этих параметров для корректировки, то можно с полной уверенностью утверждать, что течение времени в обеих системах отсчёта будет полностью синхронизировано, ведь в выражении (6) иные зависимости отсутствуют, а скорость взаимного движения систем отсчёта одинакова!

Учитывая к тому же, что интервалы равномерного движения корабля значительно превышают интервалы ускоренного движения и, в зависимости от выполняемых задач, могут быть сделаны неограниченно большими (во всяком случае теоретически), то общее старение космонавта не должно подчиняться зависимости от общего времени полёта, как это предсказывает релятивистская концепция Эйнштейна.

Именно эта проблема заставила релятивистов сделать системы отсчёта близнецов неидентичными, тем самым нарушив принцип относительности Маха и принцип относительности самого Эйнштейна, на основе которого он постулировал постоянство скорости света во всех системах отсчёта:

"Для описания того, что отсюда следует с точки зрения одного и другого близнеца, мы должны выйти за пределы СТО и обратиться к общей теории относительности, которая даёт последовательный метод рассмотрения также и состояния ускоренного движения. Тем не менее, СТО даёт "правильный ответ", если явление описывается в инерциальной системе отсчёта, и в такой системе брат, остающийся дома, оказывается старше своего странствующего брата" [Пановский: 15, с. 208- 209].

В числе прочего, хочется обратить внимание на само построение цитаты Пановского. Это характерный для релятивистов стиль отвлечения внимания от проблемы. Сначала он заявляет, что проблема решается методами ОТО вне рамок СТО, прекрасно понимая, что ускоренные интервалы не могут впрямую серьёзно повлиять на замедление времени из-за их непродолжительности. Но затем добавляет, что проблема решается и в рамках СТО, из рамок которой релятивисты вынуждены выйти для разрешения парадокса. Однако парадокс неразрешим и в рамках ОТО, и это тоже несложно показать.

Чтобы это понять, рассмотрим проблему не двух, а трёх наблюдателей A, B и C, первые два из которых являются знакомыми нам близнецами, а о третьем наблюдателе C близнецам неизвестно (любимый аргумент релятивистов ограничения возможностей наблюдателя), но который наблюдает за близнецами с целью проверки скорости течения времени.

Далее пусть события развиваются по стандартному сценарию. Близнец A готовится к полёту и сверяет свои часы с наблюдателем B. После этого A стартует с ускорением a и в течение некоторого времени t достигает скорости, сравнимой со скоростью света (допустим, v = 0,5 c). Как было процитировано выше, релятивисты уверены, что учёт данного интервала движения космонавта полностью объясняет парадокс часов. Допустим, что частота часов в данном интервале изменяется в согласии с релятивистской концепцией. Тогда, согласно Эйнштейну,

"Если излучение, испускаемое в равномерно ускоренной системе отсчёта K ' на S₂ по направлению к S₁, имело относительно находящихся в S₂ часов частоту f₂, то по прибытии в S₁ оно имеет относительно находящихся там точно таких же часов уже частоту не f₂, а б'ольшую частоту f₁, которая в первом приближении равна

"

(где - ускорение в поле тяготения, h - расстояние между S₂ и S₁) [Эйнштейн: 16, с. 170].

На основе этого выражения В. Паули получил закономерность, связывающую время в ускоряющейся системе отсчёта  t с временем неподвижного наблюдателя  [Паули: 12, п. 53, с. 221]:

где = h - потенциал тяготения, эквивалентный ускорению часов близнеца A.

"Уравнение (8) имеет следующий физический смысл: если одни из двух покоящихся, одинаковых и в начале синхронных часов поместить на некоторое время в гравитационное поле, то после этого оба прибора уже не идут синхронно, а напротив, побывавшие в гравитационном поле часы отстают. Как указал Эйнштейн [17], на этом основывается также объяснение … парадокса с часами" [Паули: 12, с. 221- 222].

Возможно, подобные толкования парадокса и были бы приемлемы, если бы не два принципиально важных момента. Во-первых, выражение (8) не соответствует формуле замедления времени в СТО, которая имеет вид

Причём различие существенно и может быть преодолено только при малых скоростях, в то время как формулу (9) релятивисты используют для объяснения замедления времени для релятивистских частиц. Во-вторых и главное, замедление времени в выражении (8) справедливо только в интервале ускоренного движения. При окончании этого временного интервала потенциал должен обратиться в ноль, в обратном случае процесс ускорения продолжится. Но при обращении в ноль потенциала, как видно из самой формулы (8), различие между течением времени в системах отсчёта близнецов аннулируется.

Таким образом, если и будет изменение скорости течения времени согласно ОТО, то оно будет ограничено только короткими интервалами ускоренного движения. А поскольку мы можем сделать интервалы равномерного движения произвольными, то соответствия между расчётами на основе СТО и ОТО не будет. Следовательно, вышеприведенное утверждение Пановского "Тем не менее, СТО даёт "правильный ответ", если явление описывается в инерциальной системе отсчёта" [Пановский: 15] некорректно