|
т.7 No
1 |
3 |
| Диалог о
сохранении энергии и импульса |

|
ВЛАДИМИР: Я не против
предлагаемого Вами подхода, уважаемый Сергей,
только боюсь, как бы не получилось чего-то типа
“из пушки по воробьям”  . А боюсь я вот по
каким основаниям. . А боюсь я вот по
каким основаниям.
Вы пишете, что “релятивистов не
интересует сам факт перехода, но вполне
устраивает факт выполнения законов динамики в
системе отсчета, свободно падающей в однородном
гравитационном поле”.
Я согласен с тем, что их это не
интересует, но “не интересует” – это, по моему,
слишком мягко сказано. Задача, которую ставил
перед собой Эйнштейн, принимаясь за ОТО,
заключалась, как я понимаю, именно в том, чтобы
убрать, дезавуировать, предать забвению то
положение классической физики, согласно
которому свободное движение тел в пространстве и
времени и их движение там же, но под действием
сил, являются принципиально различными
движениями. Согласно их логике никакого
“перехода” просто нет и быть не может.
Это в классической механике
рассматриваются “кинематика” и “динамика”.
Это классическая физика кричит “караул”, когда
видит, что воцаряется такая теория, как СТО – по
сути, чисто кинематическая, вернее, такая,
которая чисто математически и потому
безжалостно подходит к проблеме
пространства-времени и лепит из них “под себя
любимую” 4-х континуум (!) по определенным
правилам (!), в угоду выполнению заложенных в неё
постулатов. Крик “караул” вырывается в том
числе и потому, что постулаты эти, как верно
отмечаете и Вы, “кинематические”, но не
“динамические”, хотя пионерская работа и
называлась “К электродинамике …”, но вот именно
“К …”  . .
Поэтому мне кажется, – может
быть я и неправ, – что и здесь, вламываясь в поля
тяготения, они заботились больше о кинематике,
чем о динамике, поскольку о динамике они не
думали и не имели её, если честно, уже в СТО.
Пришлось постулировать экстравагантности типа
"переход энергии в массу" и т.п. "чудеса"
 . .
СЕРГЕЙ: Полностью согласен.
ВЛАДИМИР: То есть, не думаете ли
Вы о релятивистах слишком хорошо, если
предполагаете, что их волновал факт выполнения
или невыполнения законов динамики в НСО? Почему
тогда их не волнует невыполнение этих законов в
СТО? Я думаю, что у релятивистов просто нет
проблемы “перехода” из ИСО в НСО, поскольку их
принцип заключается как раз в том, что эти
системы отсчета равноправны. Сделав столь мощную
заявку, они чисто волевым усилием освободили
себя от необходимости думать о том, как
переходить из системы в систему. Все ж вокруг
"народное", все вокруг моё! 
СЕРГЕЙ: Таким образом,
уважаемый Владимир, как я и говорил с самого
начала, вопрос правомерности релятивистской
концепции лежит не в плоскости физики, а в
плоскости клановых интересов и психологии. И Вы
сейчас это подтверждаете.
Вы безусловно правы,
предполагая, что релятивистам ничего нельзя
доказать. И добавлю, невозможность проистекает
из того, что они сами уже очень давно убедились в
абсурдности своей собственной концепции.
Фактически сложилась ситуация, аналогичная
описанной Ильфом и Петровым в “Золотом
теленке”, при распиливании золотых гирь Шурой и
Паниковским:
“– Что такое! – сказал вдруг
Балаганов, переставая работать. – Три часа уже
пилю, а оно все еще не золотое.
Паниковский не ответил. Он уже
все понял и последние полчаса водил ножовкой для
виду.
– Ну-с, попилим еще! – бодро
сказал рыжеволосый Шура.
– Конечно, надо пилить, –
заметил Паниковский, стараясь отодвинуть
страшный час расплаты.
Он закрыл лицо ладонью и сквозь
растопыренные пальцы смотрел на мерно
двигающуюся широкую спину Балаганова.
– Ничего не понимаю! – сказал
Шура, допилив до конца и разнимая гирю на две
яблочные половины. – Это не золото!
– Пилите, пилите, – пролепетал
Паниковский.
Но Балаганов, держа в каждой
руке по чугунному полушарию, стал медленно
подходить к нарушителю конвенции.
– Не подходите ко мне с
этим железом! – завизжал Паниковский, отбегая в
сторону. – Я вас презираю!” [с. 191].
Не правда ли, знакомое
поведение, проявляющееся в манерах релятивистов?
И сейчас, когда постепенно начинается
отрезвление от абсурда, навязанного
релятивистами науке, часть из них, не столь
воинственная и не потерявшая меру предела в
отстаивании догмата как такового, уходит в
другие сферы деятельности и исчезает с арены
баталий, так сказать, по-английски, не
попрощавшись. Но самые “последовательные”
безусловно будут требовать продолжать пилить до
конца.
Не в них дело. Это все
постепенно уляжется. Понимание ошибочности
релятивистских подходов важно с точки зрения
того, чтобы развивая классический формализм в
область высоких скоростей и энергий, не
повторять их ошибки, к чему в настоящее время
наблюдается тенденция у сторонников эфирных
концепций, полагающих, что можно частично
заменить наиболее выпячивающие противоречия
релятивизма и сохранить фантазии типа фотонных
представлений, трансформации времени,
искривления пространства-времени в эфирной
теории, замены динамического описания процессов
кинематическим, – о чем Вы совершенно верно
пишете, – и кризис релятивизма будет преодолен.
Нет, пока все ошибки не выявлены и все абсурдные
утверждения, как и следствия, на них построенные,
не изъяты из моделей, кризис будет продолжаться,
порождая все новых и новых монстров в новой
пострелятивистской инкарнации.
Поэтому я, с Вашего позволения,
вернусь к обещанному анализу правомерности
постулирования эквивалентности законов
кинематики и динамики в рамках формализма
релятивисткой концепции.
Прежде чем мы приступим к
анализу правомерности введения эквивалентности
между выполнением законов динамики в
инерциальной и свободно падающей системах
отсчета, давайте выявим подводные камни, которые
нам встретятся и которые нам желательно обойти.
Главным подводным камнем является то, что в
рамках СТО формально не определен переход из
инерциальной системы отсчета в неинерциальную.
Как Вы помните, в рамках
классического формализма мы легко это
осуществляли кинематически, поскольку ни
временные, ни пространственные параметры при
преобразованиях не трансформировались. А
главное, скорость света не привязывалась жестко
к каждой системе отсчета и значение ее
получалось как следствие свойств галилеевых
преобразований. При этом значение скорости света
могло оставаться тем же, или становиться
анизотропным, могло изменяться распределение
эквифазных поверхностей, но все это не влияло на
остальные явления и материальные тела. Иными
словами, хотя мы регистрируем явления при помощи
света, но свойства света не имеют влияния на
физические свойства других материальных тел и
тем более на геометрию пространства и свойства
времени. В релятивизме постулат Эйнштейна о
постоянстве скорости света справедлив
исключительно в инерциальных системах отсчета и
свойства света прямо влияют на свойства
пространства и времени, как и на геометрические
размеры тел. Доказать же справедливость этого
постулата в случае, когда тела в движущейся
системе отсчета ускоряются различно –
невозможно, и с классической точки зрения
понятно почему. Потому, что даже при малых
скоростях и ускорениях скорость света в
неинерциальных системах отсчета не будет
постоянной и вариантов “очевидности” (когда
предполагается классическая очевидность, а
реализуется эта очевидность в релятивистском
формализме) Эйнштейн не нашел, да и не мог найти,
потому что дороги нет к этой очевидности и в
классическом формализме. Не на чем, так сказать,
наездничать. Именно поэтому, когда Эйнштейн
сталкивался с необходимостью ускоренного
движения, и в особенности с необходимостью
переходить в ускоренную систему отсчета, он
“уходил” на некоторые приближения, сводя
ускоренную систему отсчета к “локально
инерциальной во времени” – собственно, тот же
прием, которым он многократно пользовался при
связывании ОТО с СТО. Уже в первой своей работе
“К электродинамике движущихся тел” Эйнштейн
следующим образом определяет постановку задачи,
связанную с ускорением электрона во внешнем
поле: “Пусть в
электромагнитном поле движется точечная частица
с электрическим зарядом  (в дальнейшем называемая
“электроном”), о законе движения которой мы буде
предполагать только следующее. (в дальнейшем называемая
“электроном”), о законе движения которой мы буде
предполагать только следующее.
Если электрон
находится в покое в течение определенного
промежутка времени, то в ближайший за ним момент
времени движение электрона, поскольку оно
является медленным (!
–Сергей) будет
описываться уравнениями: |
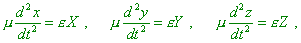 |
(d1.11) |
где x, y, z
– координаты электрона, а  – масса электрона. – масса электрона.
Далее, пусть электрон в
течение определенного промежутка времени
обладает скоростью v (заметим, что в данной постановке задачи
электрон обладает не мгновенной скоростью v
, как это полагается в ускоренном движении, а
некоторой постоянной скоростью в течение пусть и
малого, но промежутка времени – Сергей). Найдем закон,
согласно которому электрон движется в
непосредственно следующий за этим промежутком
элемент времени.
Не ограничивая
общности рассуждений, мы можем допустить и
допустим на самом деле, что в тот момент, когда мы
начинаем наблюдение, наш электрон находится в
начале координат и движется вдоль оси X
системы K со скоростью v . В таком
случае ясно, что в указанный момент времени (t
= 0) электрон находится в покое относительно
координатной системы k , движущейся
параллельно оси X с постоянной скоростью v
” [А. Эйнштейн, К
электродинамике движущихся тел, собр. соч., т. 1, с.
32].
Прочитав эту постановку задачи,
я думаю, Вы согласитесь со мной, что утверждение
Эйнштейна о замене мгновенной скорости на
некоторую постоянную во временном интервале
скорость, как и ограниченность малыми скоростями
и ускорениями, существенно ограничивает
общность, и тем более не позволяет заменять
ускоренную систему отсчета некоторой
инерциальной системой, пусть и на малом
промежутке времени. Это, кстати, отражается и на
правомерности приложения полученных в данном
приближении решений к околосветовым скоростям.
Решения, даже в случае их правильности, применимы
только к малым скоростям. Поэтому когда
релятивисты пытаются решать
электродинамические задачи для заряженных тел
на околосветовых скоростях, они автоматически
выходят за рамки правомерности эйнштейновского
математического аппарата и тем самым
автоматически делают свои решения
некорректными.
Также, я думаю, вы уже понимаете,
почему Эйнштейн решился на подобный шаг, заменив
неинерциальную систему отсчета инерциальной.
Конечно, это связано с неопределенностью
сохранения постулата о постоянстве скорости
света в ускоряющейся системе отсчета. Причем
ускоряющейся не в однородном гравитационном
поле, а в некотором произвольном
электромагнитном поле.
В ту же самую неопределенность,
думаю, не следует попадать и нам с Вами. Тем более,
как Вы увидите ниже, необходимости в этом нет.
Мы можем для начала проверить
сохранение законов динамики при переходе не из
инерциальной системы отсчета в неинерциальную, а
между инерциальными системами отсчета. Ведь
безусловно, что если Эйнштейн записывал (d.1.11) в
исходной инерциальной системе в форме закона
Ньютона, и при этом естественно предполагал
некоторую произвольность задания самой системы
отсчета, то тем самым он предполагал, что в рамках
релятивистской концепции этот закон справедлив
во всех релятивистских инерциальных системах
отсчета. Следовательно мы можем в качестве
исходного пункта проверки корректности законов
динамики в релятивистской концепции рассмотреть
простой случай воздействия постоянной
сосредоточенной силы на некоторое тело массой m
.
Внешне может показаться, что мы
будем повторять задачу об ускорении электрона.
Но это не так. Прежде всего, в эйнштейновской
задаче на электрон воздействовало поле, в
котором могли возникать и исчезать
дополнительные поля. Здесь мы рассматриваем
сосредоточенную постоянную силу и при переходе
из одной инерциальной системы отсчета в другую,
также инерциальную систему отсчета, появление
дополнительных полей абсурдно, ибо это будет как
раз нарушать законы сохранения, не так ли?
Во-вторых, подвижная система отсчета в случае
электрона обладала квазиинерциальностью только
в малом промежутке времени. В нашем случае
инерциальность неподвижной и подвижной систем
отсчета не ограничена во времени, а
следовательно, мы имеем возможность проследить
характер траектории тела на значительном
временном интервале, не выходя за рамки модели.
Наконец, в-третьих, Эйнштейн сразу предполагал,
что в подвижной системе отсчета справедлив
второй закон Ньютона, и из этого исходил в своих
построениях. Мы не берем на себя ответственность
заранее предполагать сохранение законов
классической физики при переходах между
системами отсчета в рамках релятивистского
формализма. Чтобы избежать необходимости
преобразовывать закон Ньютона при помощи
преобразований Лоренца, уподобляя вектор силы
вектору скорости, мы можем воспользоваться тем
обстоятельством, что по признанию самих
релятивистов, неподвижная система отсчета
классической механики идентична неподвижной
системе отсчета релятивистской механики: “Релятивистская
механика исходит из предположения, что в системе
координат K' , в которой материальная точка в
рассматриваемый момент покоится, справедливы
уравнения движения старой механики” [В. Паули, Теория
относительности, с. 170]. Если к этому добавить, что
согласно постановке задачи в работе Эйнштейна,
цитированной выше, закон Ньютона по его мнению
справедлив и в системе отсчета, по отношению к
которой материальная точка (в данном случае
электрон) движется, то мы можем на основании
второго закона Ньютона сразу записать
траекторию движения тела и далее
преобразовывать не силы, а траекторию,
предполагая, что наблюдение за ускоренным
движением тела в подвижной инерциальной системе
отсчета по связанной с ней мерам и часам ничем не
отличается от технологии наблюдения за
равномерно движущимся телом. Опираясь на эту
методику, мы получаем возможность сравнить
характер движения тела в неподвижной и подвижной
системе отсчета, не предполагая заранее закон
ускорения тела в подвижной системе отсчета под
воздействием силы, и анализировать соблюдение
базового закона динамики по сравнимости
характеров траектории движения. Ведь если
характер изменения скорости и ускорения при
переходе из одной системы в другую сохранится, то
сохранится и характер воздействия силы. Если же
характер изменения скорости и ускорения
изменится, то это естественно означает и
изменение закона воздействия силы. И чтобы
выявление сохранения или несохранения закона
динамики проявлялось более четко, мы не будем
предполагать, что в неподвижной системе отсчета
масса тела изменяется с его скоростью.
Итак, с учетом предварительных
условий, предположим, что в некоторой
неподвижной (нештрихованной) системе отсчета
вдоль оси x движется тело A массой m
с постоянным ускорением a . Причем, исходя из
определенной произвольности выбора неподвижной
системы отсчета, предположим, что в начальный
момент времени t0 = 0 тело
находилось в начале координат, т.е. x0 = y0 = z0 = 0 ,
и скорость тела в данный момент была тоже равна
нулю, т.е. u0 = 0 . Поскольку по условию задачи
тело движется вдоль оси x , координаты y
и z мы можем в дальнейшем не
рассматривать, т.к. они изменяться не будут.
Исходя из постановки задачи,
траектория тела будет описываться выражением |
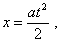 |
(d1.12) |
а его мгновенная скорость –
уравнением |
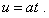 |
(d1.13) |
Чтобы получить возможность
исследовать характер движения тела в движущейся
системе отсчета, предположим, что эта
(штрихованная) система отсчета движется
относительно неподвижной системы с некоторой
постоянной скоростью v в положительном
направлении оси x и в начальный момент
времени начала координат обеих систем отсчета
совпадают, а t'0 = t0 = 0 , что
полностью соответствует начальным условиям,
обычно используемым Эйнштейном для упрощения
выкладок.
Переход из нештрихованной
системы отсчета в штрихованную будем
осуществлять с использованием стандартных
преобразований Лоренца в виде |
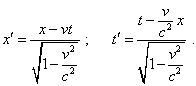 |
(d1.14) |
Подставляя (d1.12) в (d1.14), получим |
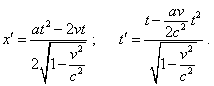 |
(d1.15) |
В полученных уравнениях (d1.15)
параметры штрихованной системы отсчета зависят
от одного временного параметра нештрихованной
системы. А следовательно, если мы избавимся от
этого последнего параметра неподвижной системы,
мы получим одно уравнение, которое описывает
характер движения тела A в физическом
времени подвижной системы отсчета. Поскольку нас
интересует стандартный вид зависимости
координат от времени, представим второе
уравнение (d1.15) в виде |
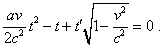 |
(d1.16) |
Решение данного квадратного
уравнения имеет вид |
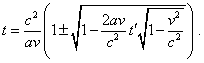 |
(d1.17) |
Чтобы (d1.17) обеспечивало
равенство t'0 = t0 = 0 в
начальный момент, из двух знаков перед корнем мы
должны выбрать минус, и таким образом решение
примет вид |
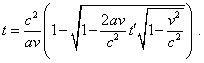 |
(d1.18) |
Теперь, подставляя (d1.18) в первое
уравнение системы (d1.15), получим |
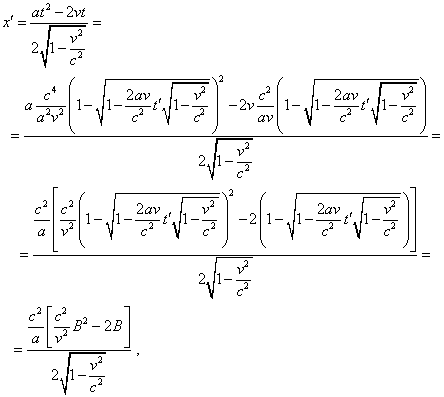 |
(d1.19) |
Полученное выражение (d1.19)
описывает искомую нами зависимость движения
исследуемого тела в подвижной системе отсчета с
точки зрения релятивистской концепции. Из
решения мы сразу видим, что время, в течение
которого тело может ускоряться, с точки зрения
подвижной системы отсчета ограничено и
определяется интервалом, на котором величина B
остается действительной величиной, в то время
как согласно (d1.12) тело может двигаться в
неподвижной системе отсчета неограниченное
время. И можно было бы говорить здесь о
невозможности движения со скоростями,
превышающими скорость света, но тогда координата
тела не становилась бы мнимой, а сохраняла бы
некоторую постоянную скорость при достижении
скорости света. Здесь же мы имеем дело с
откровенной нелогичностью преобразования,
которое предлагает нам преобразование Лоренца.
ВЛАДИМИР: Как я вижу, выражение
(d1.19) эффективно упрощается. Раскрывая скобки,
получим |
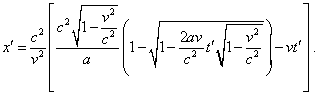 |
(d1.20) |
СЕРГЕЙ: Согласен, и это важно
для дальнейших операций с полученным решением.
Ведь нас с Вами интересует закон изменения
ускорения тела с точки зрения подвижной системы
отсчета. Вторая производная координаты по
времени в (d1.20) имеет вид |
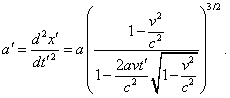 |
(d1.21) |
График, построенный на основе
выражения (d1.20), представлен на рис. 3. |
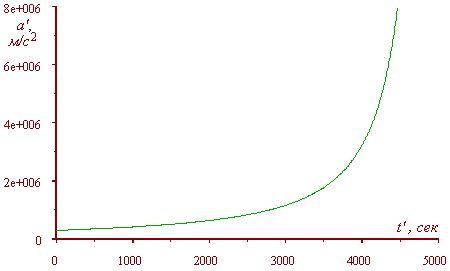
Рис. 3. График временной
зависимости ускорения тела в подвижной системе
отсчета при скорости подвижной системы отсчета v
= 0,1 c, м/сек и численном значении
постоянного ускорения тела в неподвижной
системе отсчета a = 0.001 c, м/сек2
|
И каково Ваше мнение по поводу
полученной зависимости, уважаемый Владимир?
ВЛАДИМИР: Прежде чем говорить
по поводу полученной зависимости, разрешите мне,
уважаемый Сергей, высказаться по поводу
разобранной Вами задачи. Очевидно, что тема
ускорений для релятивистов чрезвычайно
болезненна. Настоящий “гвоздь в сапоге”, причем
приличных размеров. Они, конечно, делают вид, что
никакого такого “гвоздя” нет. Например, в их
“талмуде” – Л.Д. Ландау, Е.М. Лифшиц, т. 2, “Теория
поля” – об ускорении упоминается походя,
вскользь, в нескольких строчках в конце
параграфа 7, который сам-то меньше страницы. Мол,
ускорения – это такая мелочь, что и говорить-то о
них не стоит. Все и так, дескать, понятно. При этом,
далее следует решение задачи на “релятивистское
равноускоренное движение”. Что же из него
следует? Во-первых, что с у них считается
инвариантом во всех случаях. Без всякого
доказательства. Так сказать, “жена Цезаря вне
подозрений”  . .
СЕРГЕЙ: Отмечу, уважаемый
Владимир, что и равноускоренное движение, в
сущности, в релятивистской концепции таковым не
является. Ведь в упомянутой Вами книге Л.Д. Ландау
ускорение принимается постоянным относительно
собственной системы отсчета: “Релятивистски
инвариантное условие равноускоренности должно
быть представлено в виде постоянства 4-скаляра,
совпадающего с w2 (где w
является 4-ускорением – Сергей) в
собственной (! – Сергей) системе
отсчета: |
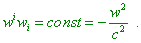 |
(d1.22) |
… В “неподвижной”
системе отсчета |
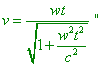 |
(d1.23) |
[Л.Д. Ландау, Е.М. Лифшиц. Теория
поля, т. 2, с. 39]. Как Вы видите, и в подсчетах
релятивистов, при всем том, что ускорение у них
уже является не вектором, а скаляром, при всем
том, что они не решают задачу впрямую, как это они
делают с равномерными скоростями (хотя, как я уже
говорил, технология наблюдения ускоренного
движения ничем не отличается от технологии
наблюдения равномерного движения), при том, что
они используют псевдоускоренную систему отсчета
путем постоянной смены инерциальных систем, не
обосновав правомерность подобного
использования, как не обосновав и правомерность
связи 4-координатного представления с условием
постоянства ускорения в этой сопутствующей
системе отсчета, – релятивисты получают
неравноускоренное движение в неподвижной
системе отсчета.
И это не является особенностью
представлений Ландау. Например, у В. Паули читаем
аналогичное определение равноускоренного
движения: “Равноускоренным
движением в релятивистской кинематике (! –
Сергей) естественно (?! – Сергей) считать такое движение, для которого
ускорение постоянно имеет одно и то же значение b в сопутствующей в данный момент
телу (! – Сергей) или материальной
точке системе координат K' . Система K' для
каждого момента – другая; в одной определенной
галилеевой системе K ускорение подобного движения не
постоянно во времени (т.е. именно то, что мы с
Вами и получили в наших расчетах – Сергей). Так обстоит дело при прямолинейном
равноускоренном движении” [В. Паули,
Теория относительности, с. 114].
Более того, под это ускорение и
4-мерный интервал у релятивистов тоже изменяется.
В случае равноускоренного движения в
неподвижной системе отсчета он уже имеет иной
вид: “Особый
интерес представляют формулы преобразования
ускорения от системы K' , мгновенно
сопутствующей телу, к системе K ,
относительно которой тело движется со скоростью u
. Если ось x направить по направлению
скорости, то для этого случая имеем… Из (194)
получаем легко интегрированием: |
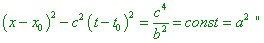 |
(d1.24) |
[В. Паули, Теория
относительности, с. 113–114].
При этом сам факт изменения
4-мерного интервала в случае ускоренного
движения свидетельствует о том, что релятивисты
не имели права распространять закономерности
равноускоренного движения на ускоренное и тем
более использовать, переходя в их так называемые
собственные системы отсчета, если в целом даже в
неускоренных системах их четырехмерный интервал
не сохраняется в исходном виде. Ведь из (d1.24)
видно, что при b = 0 , т.е. при отсутствии
ускорения в нашем понимании, правая часть (d1.24) не
становится равной c2 , ни тем более ds2,
а обращается в бесконечность. А следовательно, в
релятивизме отсутствию ускорения соответствует
условие b = c, что само по себе нонсенс,
поскольку, напоминаю, согласно релятивизму,
равноускоренным движением нужно “…считать
такое движение, для которого ускорение постоянно
имеет одно и то же значение b в
сопутствующей в данный момент телу… системе
координат K' ”.
Как видите, здесь тоже
наблюдается игра релятивистов на “очевидности”
классических представлений. Ведь когда любому
физику говорят о равноускоренном движении, он
воспринимает этот термин вполне конкретно и
связывает его с неподвижной (лабораторной)
системой отсчета, а не с системой отсчета,
сопутствующей ускоряемому телу в данный момент.
ВЛАДИМИР: Разумеется, для
кинематической теории, описывающей переходы
между ИСО (!) переход в ускоренную “сопутствующую
систему” – это "запрещенный прием". Я так
понимаю, что это примерно то же, как “закон
обратную силу имеет”, или как говорил Аркадий
Райкин, “семь пишем, три на ум пошло”. Это некие
щупальца ОТО, запускаемые из-за спины СТО. Но как
все это преподносится, выглядит смешно. Вот
только формула (d1.24) выглядит действительно
странно, поскольку отрицательная левая часть
приравнивается положительной правой. Неужели у
Паули ошибка?
СЕРГЕЙ: Сие покрыто мраком,
уважаемый Владимир. Судите сами, система
уравнений (194), на которую ссылался в цитате Паули,
имеет вид: |
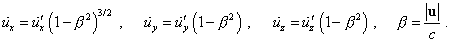 |
(d1.25) |
В свою очередь, данное
уравнение получилось у Паули в результате
совмещения двух систем уравнений для каждой
системы отсчета (с. 113 у Паули): |
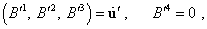 |
(d1.26) |
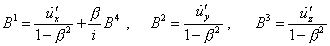 |
(d1.27) |
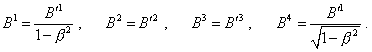 |
(d1.28) |
Подстановка (d1.26), (d1.27) в (d1.28) в
принципе должна привести к следующему выражению
для первого выражения системы (d1.25) |
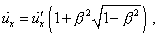 |
(d1.29) |
а не к тому, которое записано у
Паули. Но даже в случае, если у Паули первое
выражение в (d1.25) верно, а по утверждению Паули, “эти соотношения ((d1.25) – Сергей) имеются уже в первой же работе Эйнштейна
(что, признаюсь, я не нашел ни в первой, ни в
первых работах Эйнштейна – Сергей)”
[В. Паули, Теория относительности, с. 114], то с
учетом условия задачи |
первообразная должна
находиться из выражения |
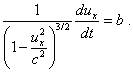 |
(d1.30) |
Согласитесь, что найти
первообразную от левой части (d1.30) не так просто, а
ведь нужно определять еще второй интеграл, и это
будет еще сложнее. Поэтому я подхожу к вопросу
очень просто. Уже не одно поколение релятивистов
воспитано на этой книге и никаких претензий к ней
пока слышно не было. Тем более, что согласно М.
Борну, левая часть (d1.24) не отрицательна: “Мы можем назвать |
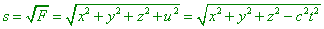 |
(d1.31) |
“четырехмерным
расстоянием”, но при этом следует помнить, что
это выражение используется лишь символически.
Отправляясь от нашего инварианта F , реальный смысл величины s нетрудно
истолковать. Ограничимся плоскостью xt (или xu);
тогда |
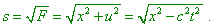 |
(d1.32) |
Далее, для всякой
пространственно-подобной мировой линии F
положителен, следовательно, s , как
квадратный корень из положительного числа, есть
действительная величина. Тогда можно сделать
мировую точку (событие) x, t
одновременной с началом путем соответствующего
выбора системы отсчета S . При t = 0 мы
имеем s = (x2)1/2 = x в роли
пространственного расстояния от мировой точки
до начала отсчета” [М.
Борн, Эйнштейновская теория относительности, с.
298–299]. Заметьте, что и в (d1.31), и в (d1.32) запись
четырехмерного интервала идентична записи у
Паули в (d1.24). Хотя безусловно Вы правы, что для
траектории материального тела разность в
приведенной записи в левой части должна быть
отрицательной при v < c . Вот такая
арифметика, уважаемый Владимир. Поэтому самое
надежное – это анализировать результаты,
представленные самими релятивистами, и этих
результатов вполне достаточно, чтобы показать
неправомерность их подходов к решению задач
физики. |
Титульная
страница: /1 / 2
/ 3 / 4 / 5 /
|
|







