|
СЕЛФ |
4 |
| Диалог о сохранении
энергии и импульса |

|
ВЛАДИМИР: Продолжая
придираться, отмечу, что Ваши рассуждения после
формулы (d1.24) я тоже не совсем понимаю, в
частности, почему это правая часть должна
равняться с2 ? Релятивисты обычно пишут s2.
А вот то, что интервал уходит в бесконечность при b,
стремящемся к нулю, надо было бы релятивистам
как-то народу объяснить.
СЕРГЕЙ: Согласен с Вами, но я
взял один из стандартных вариантов. Согласитесь,
что если я возьму, например, b = kc, k
> 1 и размерный, то получится еще хуже,
поскольку еще и ускорение по численной величине
будет больше скорости света.  Так что
релятивистам нужно объяснять не только причину
обращения правой части (d1.24)
в бесконечность при равномерном движении, но и
столь значительные величины ускорения при
равномерном движении. Так что
релятивистам нужно объяснять не только причину
обращения правой части (d1.24)
в бесконечность при равномерном движении, но и
столь значительные величины ускорения при
равномерном движении.
ВЛАДИМИР: Во-вторых, ускорение,
с их точки зрения, должно с течением времени
“подстраиваться” под ситуацию таким образом,
чтобы скорость материальной точки не могла
превысить с . То есть, ускорение у них не
является абсолютом, как в классике. Это в
классике оно хозяин ситуации, а в релятивизме оно
слуга постулата о постоянстве скорости света.
Например, в релятивистском пределе их
“ускорение” будет обратно пропорционально
текущему моменту времени в неподвижной системе
отсчета.
СЕРГЕЙ: Более того, даже при
достижении телом в неподвижной системе отсчета
скорости света, в собственной системе отсчета
ускорение тела сохранится и будет сохранять все
ту же постоянную величину, что само по себе
является нонсенсом.
ВЛАДИМИР: Я понимаю, что Вы
хотите сказать, но хочу заметить, что по
воззрениям релятивистов тело никогда не может
достигнуть скорости света. Поэтому с их точки
зрения телу предоставляется возможность
ускоряться бесконечно.
СЕРГЕЙ: С одной стороны
согласен. И Паули пишет об этом же: “Скорость
не увеличивается неограниченно, а приближается
асимптотически к скорости света.
Соответствующая мировая линия есть гипербола,
вследствие чего равноускоренное движение
релятивистской механики называют также
гиперболическим, в противоположность
“параболическому движению” старой механики” [В.
Паули, Теория относительности, с. 114]. Но давайте
посмотрим на данный вопрос с другой стороны. Если
мы в нашей задаче, в которой предполагается
переход между инерциальными системами отсчета,
установим вслед за релятивистами постоянство
ускорения в движущейся системе отсчета, то в
неподвижной системе мы тоже получим
гиперболическое ускорение движения тела.
Действительно, при a' = b = const и из
(d1.18) |
мы на основании (d1.21) получаем |
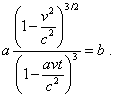 |
(d1.33) |
График данной зависимости во
времени представлен на рис. 4.
|
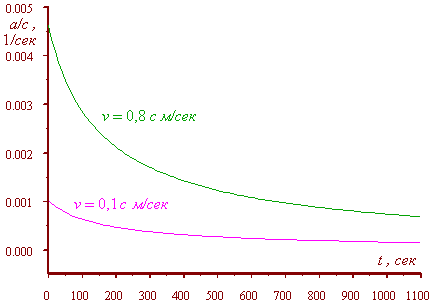
Рис. 4. График временной
зависимости ускорения тела в неподвижной
системе отсчета при постоянном ускорении тела в
подвижной системе отсчета при различных
скоростях подвижной системы отсчета и численном
значении постоянного ускорения тела в подвижной
системе отсчета b = 0,001c, м/сек2 |
Представленный график
показывает ту же самую гиперболическую
зависимость, которая уже не ограничивается
условием перехода траектории тела в комплексную
плоскость, и данное движение может длиться
бесконечно, приближая скорость тела к скорости
света.
Но теперь задумаемся над
простым вопросом. Есть две инерциальных системы
отсчета, наблюдатели которых следят за
неравномерным движением тела. В одной системе
отсчета ускорение представляется постоянным, а в
другой гиперболическим. Не является ли это
прямым ответом на поставленный нами вопрос о
неэквивалентности инерциальных систем отсчета в
релятивистском формализме?
ВЛАДИМИР: Но ведь у
релятивистов работает не (d1.13), а (d1.23).
А формулы типа (d1.11) и
(d1.13) у них называются “низкоскоростной предел”
или что-то типа этого.
СЕРГЕЙ: Согласен с Вами как
минимум в том, что релятивисты пытаются
указанным Вами способом представить получаемые
ими формулы. Но посмотрим на числитель
указанного Вами выражения (d1.23). Там стоит
произведение некоторого постоянного ускорения
на время. Причем это произведение записывается
релятивистами не в ускоренной системе отсчета. В
этой системе отсчета ускорение было бы равно
нулю, не так ли? Это постоянное ускорение
записывается в мгновенно сопутствующей системе
отсчета, которая является по сути инерциальной
системой, но в каждый момент для тела данная
инерциальная система отсчета уже новая. Но если в
каждый новый момент эта система уже новая, то
релятивисты в принципе уже не имеют права
находить ни первые, ни тем более вторые
дифференциалы от смещения, в рамках одной
системы отсчета. Они должны переводить
координаты и время из новой системы отсчета в
предыдущую, а для вторых дифференциалов они
должны использовать уже перевод из двух
последующих систем отсчета. При этом, как Вы
понимаете, ни о каком постоянстве ускорения в
собственной системе отсчета и речи уже не будет,
а будет чехарда. Тем не менее релятивисты
признают, что в инерциальной системе отсчета,
скорость которой в некоторый момент времени
совпадает со скоростью тела, имеет место
равноускоренное движение. А следовательно и во
второй, и в третий моменты времени данное
ускорение наблюдается из этой же инерциальной
системы отсчета. Только в этом случае, кстати,
вообще можно говорить об ускорении тела
относительно конкретной системы отсчета. И если
в эти три момента времени было зафиксировано
ускорение тела в одной системе отсчета, то можно
утверждать, что было зафиксировано и равномерное
ускорение тела в этой же инерциальной системе
отсчета. Действительно, пусть собственная
система отсчета сохраняется в течение двух
интервалов времени dt'1 = dt'2
(три фиксированных момента времени), и в эти два
интервала времени тело последовательно
сместилось на расстояние dl'1 и dl'2
. Наличие этих данных позволяет нам определить
ускорение b в этой сопутствующей системе
отсчета, не так ли? И без этих дифференциалов
Паули, как и все остальные релятивисты, не имел бы
права записывать  'x , 'x ,  'y , 'y ,  'z в (d1.27), не так ли? Но как бы ни
были малы приращения времени и координат
смещения тела в данной собственной инерциальной
системе отсчета, мы всегда можем образовать еще
меньшие бесконечно малые приращения, записав 'z в (d1.27), не так ли? Но как бы ни
были малы приращения времени и координат
смещения тела в данной собственной инерциальной
системе отсчета, мы всегда можем образовать еще
меньшие бесконечно малые приращения, записав  t'1 = dt'1/n
, t'1 = dt'1/n
,  t'2
= dt'2/n , и на этих приращениях
определить ускорение тела, которое тоже будет
равно b . Следовательно, в рамках общего
бесконечно малого приращения времени мы можем n
раз провести измерение ускорения тела в
данной системе отсчета и выявить постоянство
этого ускорения относительно данной системы
отсчета, прежде чем будет введена новая
собственная система отсчета. И если данное
постоянство сохраняется в течение бесконечно
малого интервала времени без тех трансформаций,
которые, по утверждению релятивистов, приводят к
гиперболическому характеру ускорения, то можно с
уверенностью говорить о том, что при сохранении
характера движения тела в последующие
промежутки времени в данной конкретной
инерциальной системе отсчета (которая была
краткое мгновение собственной системой отсчета
тела) движение тела останется равноускоренным, а
значит, как минимум в этой СО классическая
формула сохранится. А исходя из идентичности
всех ИСО, эта формула сохранится и для остальных
систем отсчета. Таким образом мы видим, что в
инерциальной системе отсчете сохраняется
классическое выражение, описывающее
равноускоренное движение. Все остальное уже
является переворачиванием релятивистами
математического формализма под свои желания. t'2
= dt'2/n , и на этих приращениях
определить ускорение тела, которое тоже будет
равно b . Следовательно, в рамках общего
бесконечно малого приращения времени мы можем n
раз провести измерение ускорения тела в
данной системе отсчета и выявить постоянство
этого ускорения относительно данной системы
отсчета, прежде чем будет введена новая
собственная система отсчета. И если данное
постоянство сохраняется в течение бесконечно
малого интервала времени без тех трансформаций,
которые, по утверждению релятивистов, приводят к
гиперболическому характеру ускорения, то можно с
уверенностью говорить о том, что при сохранении
характера движения тела в последующие
промежутки времени в данной конкретной
инерциальной системе отсчета (которая была
краткое мгновение собственной системой отсчета
тела) движение тела останется равноускоренным, а
значит, как минимум в этой СО классическая
формула сохранится. А исходя из идентичности
всех ИСО, эта формула сохранится и для остальных
систем отсчета. Таким образом мы видим, что в
инерциальной системе отсчете сохраняется
классическое выражение, описывающее
равноускоренное движение. Все остальное уже
является переворачиванием релятивистами
математического формализма под свои желания.
И наконец, говоря о возникающих
противоречиях, я хотел бы еще раз обратить Ваше
внимание на представленный рис. 4. На нем Вы
видите зависимость ускорения в неподвижной
системе отсчета при двух значениях скорости
подвижной системы отсчета, при том условии, что в
каждой из этих систем отсчета ускорение
постоянно. Но что означает величина ускорения в
неподвижной системе отсчета? Не то ли, что мы ее
измеряем именно в этой системе, а не через
посредство других систем отсчета? А если так, то
согласно релятивистскому представлению
получается, что в зависимости от того, какую
вспомогательную виртуальную систему отсчета мы
возьмем, такое значение ускорения измерим в
неподвижной системе отсчета. И поскольку
подобных виртуальных систем бесконечное
множество, включая и движущиеся со скоростями,
близкими к скорости света, то мы оказываемся
неспособными измерить даже малое ускорение, взяв
в качестве виртуальной систему отсчета,
движущуюся со скоростью, близкой к скорости
света. Нонсенс. Абсурд, который проистекает из
неспособности релятивистской концепции
описывать ускоренные движения, вследствие чего
релятивистам нужно измерять и задавать
ускорения не непосредственно в некоторой
системе отсчета, а через некоторую промежуточную
систему, относительно которой они также не могут
выполнить условия своего формализма с требуемой
в математике строгостью.
ВЛАДИМИР: Тем не менее, я думаю,
что в данном случае “признание” самих
релятивистов, что неподвижная система отсчета
классической механики идентична неподвижной
системе отсчета релятивистской механики: “Релятивистская механика исходит из
предположения, что в системе координат K' , в
которой материальная точка в рассматриваемый
момент покоится, справедливы уравнения движения
старой механики” [В. Паули, Теория
относительности, с. 170] роли не играет, поскольку
это сделано, видимо, недостаточно
обдуманно. Основная часть релятивистов очевидно
так не думает. Например, потому, что (d1.13)
обуславливает неограниченный рост скорости, а
для релятивизма это неприемлемо.
СЕРГЕЙ: То, что релятивистам
привычно нарушать условия и границы
применимости как своего формализма, так и
заимствованного, – не новость. Но все формулы,
связанные с ускорением и релятивистской
динамикой, построены на том принципе и тех
ограничениях, которые вынуждены были установить
сами отцы релятивизма, не видя возможности
согласовать решения с феноменологией более
общим образом, и все ограничения в случае
ускоренного движения сводятся к малым скоростям,
чтобы иметь возможность хотя бы приближенно
создать видимость той самой “очевидности”
использования формализма классической механики
в релятивистской кинематике. Если бы Эйнштейн
этого ограничения не сделал, то ему пришлось бы
полностью повторять всю работу многих и многих
поколений ученых по созданию динамики, да к тому
же в отсутствие экспериментальной базы, которая
давала бы основания вводить ту или иную
закономерность между действующей силой, массой
тела и ускорением. Не зря же все постулаты
релятивизма обосновываются очевидностью с точки
зрения классической физики и теории Максвелла.
ВЛАДИМИР: Ваше заявление, что
“в неподвижной системе отсчета релятивистская
кинематика принимается идентичной
классической”, совершенно верно. Но динамика,
как гласит классика, совсем не кинематика и
перенос сюда “идентичности” при помощи (d1.12) не представляется
обоснованным, даже если релятивисты иногда
путают динамику с кинематикой. Подумайте,
уважаемый Сергей, может быть есть смысл остаться
именно в низкоскоростном пределе, чтобы не столь
сильно противоречить формализму СТО. Основные
закономерности рисунков, я думаю, останутся.
СЕРГЕЙ: Дело ж не в
закономерностях рисунков, уважаемый Владимир, я
потому до рассмотрения задачи и предупреждал,
что нужно остерегаться неопределенности,
связанной с формализацией релятивистами
ускоренной системы отсчета. В нашем же примере,
который мы с Вами рассмотрели, применяется
фактически только описание траектории с точки
зрения двух инерциальных систем отсчета и
сведение релятивистами же законов кинематики в
одной системе отсчета к классической механике.
Второй вопрос является только внешне проблемным,
поскольку, как я Вам уже показал, не задав хотя бы
в одной системе отсчета законы, релятивисты не
способны записать эти законы в другой системе
отсчета. И запись они вынуждены вести именно в
той форме, в которой это делает классическая
механика. При этом, заметьте, при описании
ускоренного движения релятивисты
ограничиваются связью между собственной и
неподвижной системой отсчета. Но ведь точно так
же мы можем наблюдать ускоренное движение из
двух инерциальных систем отсчета, не так ли?
Причем это значительно более часто
встречающаяся в моделировании ситуация. Но
релятивисты не отвечают на этот вопрос, и молчат
потому, что данный переход с помощью их
собственной системы отсчета невозможен. Судите
сами. Подобная связь может образовываться
исключительно через собственную систему
отсчета, которая задает тот самый
гиперболический релятивистский характер
движения тела. Выше я записал эту связь между
трехмерными ускорениями неподвижной и
собственной систем отсчета (d1.25). В каждое
выражение входит параметр  , значение которого зависит
от мгновенной скорости тела, связанного с
изменением скорости последовательности
собственных систем отсчета. Т.е. во времени этот
параметр сам по себе отражает ускоренный
характер движения тела. Если неподвижная
инерциальная система отсчета одна, то у Паули, по
его утверждению, не было больших проблем с
зависимостью , значение которого зависит
от мгновенной скорости тела, связанного с
изменением скорости последовательности
собственных систем отсчета. Т.е. во времени этот
параметр сам по себе отражает ускоренный
характер движения тела. Если неподвижная
инерциальная система отсчета одна, то у Паули, по
его утверждению, не было больших проблем с
зависимостью  от времени, хотя он обязан был
учитывать функциональный характер этого
параметра при нахождении первообразной. Но если
мы имеем две инерциальные системы отсчета,
движущиеся с различными скоростями друг
относительно друга, из которых наблюдаем за
ускоренным движением тела, то чтобы перейти из
одной системы отсчета в другую, нам необходимо
преобразовать одно значение временизависимого
значения от времени, хотя он обязан был
учитывать функциональный характер этого
параметра при нахождении первообразной. Но если
мы имеем две инерциальные системы отсчета,
движущиеся с различными скоростями друг
относительно друга, из которых наблюдаем за
ускоренным движением тела, то чтобы перейти из
одной системы отсчета в другую, нам необходимо
преобразовать одно значение временизависимого
значения  в другое. Думаю, не только мы не знаем
подобного способа, но и релятивисты корректного
способа не подскажут, потому что его нет из-за
непостоянства этого параметра во времени.
Обычный же способ суммирования скоростей
неприменим, поскольку закон параллелограмма в
релятивистской концепции не работает даже для
постоянных скоростей, не говоря уже о сложении
инерциального и равноускоренного движений.
Судите сами, пусть Вы наблюдаете это самое
гиперболическое движение из неподвижной системы
отсчета, но решили воспользоваться при расчетах
не прямой формулой, а выражением, полученным с
использованием некоторой произвольно Вами
введенной виртуальной системы отсчета. В
классическом формализме это, как Вам хорошо
известно, не приведет ни к каким проблемам. Здесь
же, как показано в п. 7.1.5 работы, в зависимости от
выбранной Вами скорости этой виртуальной
системы отсчета, Вы можете получить любое
значение исследуемой скорости, и даже больше
скорости света. А если справедливы только прямые
измерения, вследствие неоднозначности
суммирования скоростей в релятивистской
кинематике, то и связывать инерциальные системы
отсчета при наблюдении ускоренного движения
неправомерно – именно вследствие указанной
неправомерности самой формулы сложения
скоростей.
в другое. Думаю, не только мы не знаем
подобного способа, но и релятивисты корректного
способа не подскажут, потому что его нет из-за
непостоянства этого параметра во времени.
Обычный же способ суммирования скоростей
неприменим, поскольку закон параллелограмма в
релятивистской концепции не работает даже для
постоянных скоростей, не говоря уже о сложении
инерциального и равноускоренного движений.
Судите сами, пусть Вы наблюдаете это самое
гиперболическое движение из неподвижной системы
отсчета, но решили воспользоваться при расчетах
не прямой формулой, а выражением, полученным с
использованием некоторой произвольно Вами
введенной виртуальной системы отсчета. В
классическом формализме это, как Вам хорошо
известно, не приведет ни к каким проблемам. Здесь
же, как показано в п. 7.1.5 работы, в зависимости от
выбранной Вами скорости этой виртуальной
системы отсчета, Вы можете получить любое
значение исследуемой скорости, и даже больше
скорости света. А если справедливы только прямые
измерения, вследствие неоднозначности
суммирования скоростей в релятивистской
кинематике, то и связывать инерциальные системы
отсчета при наблюдении ускоренного движения
неправомерно – именно вследствие указанной
неправомерности самой формулы сложения
скоростей.
Поэтому, решая задачу путем
непосредственного наблюдения траекторий
движения тела с точки зрения двух систем отсчета
и задания траектории движения в одной из
инерциальных систем отсчета, мы с вами обошли
многие проблемы релятивистской механики, и наше
рассмотрение, в отличие от способа решения
задачи самими релятивистами, не ограничивается
пределом v << c . Это обусловлено
правомерностью применимости самих
преобразований Лоренца вплоть до световых
скоростей. Также мы полностью имели право
исследовать поточечно любые траектории, в том
числе и траекторию, описывающую равноускоренное
движение. И то, что релятивисты сами же
используют классические формулы для определения
ускорения в инерциальных собственных системах
отсчета, позволяет нам также пользоваться этими
формулами в инерциальных же системах отсчета. А
то, что при этом в релятивистской концепции
возникают проблемы, так они и без этого возникают
в вопросах, связанных с ускоренным движением
тела.
ВЛАДИМИР: Признаюсь, что
довольно много времени мне понадобилось для
того, чтобы уяснить, что Вы рассматриваете только
низкоскоростной предел (v << c).
СЕРГЕЙ: И как я Вам показал, я
вынужден был идти по чуть заметной тропке между
противоречиями внутри самой релятивистской
концепции.
ВЛАДИМИР: Не знаю, насколько
корректно брать преобразования координат в
точном виде, а выражения для ускорения в
предельном. Поэтому, когда Вы написали
“Подставляя (d1.12) в (d1.14)”, я долго думал, что
Вы совершаете “смертный грех”, но потом решил,
что ничего страшного и надо посмотреть, что из
этого получится.
СЕРГЕЙ: Конечно, никакого греха
я не совершил, хотя бы потому, что если бы в (d1.12)
стояло уравнение равномерного движения тела, то
никакого смертного греха ни Вы, ни релятивисты не
усмотрели бы, учитывая к тому же, что закон
сложения релятивистских скоростей основан
именно на преобразовании равномерного движения
тела относительно подвижной системы отсчета в
соответствующее движение относительно
неподвижной системы отсчета. Действительно,
постановка задачи для нахождения выражения
суммирования релятивистских скоростей у
Эйнштейна имела следующий вид: “Пусть в системе k
, движущейся со скоростью v вдоль оси X
системы K , движется точка согласно
уравнениям |
где w и w и w – постоянные. – постоянные.
Найдем движение точки
относительно системы K . Если в уравнения
движения точки с помощью введенных в п. 3 формул
преобразования (стандартные
преобразования Лоренца – Сергей) ввести величины x, y, z,
t , то получим |
[А. Эйнштейн. К электродинамике
движущихся тел, т. 1, с. 20].
Как Вы можете видеть, уважаемый
Владимир, ход решения в случае равномерного
движения тела аналогичен примененному нами в
задаче о равноускоренном движении. Так же
задается закон движения тела в одной
инерциальной системе отсчета и подставляется в
преобразования Лоренца для нахождения
траектории движения тела в другой инерциальной
системе отсчета.
Проблемы появляются у
релятивистов в связи с их постулатом о
постоянстве скорости света, и в связи с этим, как
Вы могли видеть, в той же инерциальной системе
отсчета 4-мерный интервал изменяется всего лишь
вследствие того, что в данной системе находится
ускоряющееся тело. В связи с этим возникает очень
простой и закономерный вопрос о зависимости
метрики пространства в релятивистской ИСО от
того, что одни тела движутся в этой ИСО
инерциально, а другие с ускорением. “Хорошая”,
замечу я Вам, инвариантность 4-интервала.  Ведь вдумайтесь в сам термин “инвариантность”
– отсутствие вариантов изменения. А тут всего
лишь появление какого-то ускоренного тела, и
интервал в ИСО уже приобретает совсем другой вид.
Причем для инерциальных движений он остается
прежним, а для ускоренных движений нужно уже
использовать иные, специальные меры. Само это уже
свидетельствует о том, что эквивалентности
законов в релятивизме не существует даже между
инерциальными системами отсчета. Ведь не следует
забывать, что вводя относительность, релятивисты
особый упор делают на то, что они определяют
метрику пространства по измеримости теми мерами,
которые неподвижны в соответствующей системе
отсчета. И если для одних движений у них одни
меры, а для других движений – другие, то и меры
как таковой в релятивизме уже нет, и после этого
фактически становится бессмысленной вся их
математика.
Ведь вдумайтесь в сам термин “инвариантность”
– отсутствие вариантов изменения. А тут всего
лишь появление какого-то ускоренного тела, и
интервал в ИСО уже приобретает совсем другой вид.
Причем для инерциальных движений он остается
прежним, а для ускоренных движений нужно уже
использовать иные, специальные меры. Само это уже
свидетельствует о том, что эквивалентности
законов в релятивизме не существует даже между
инерциальными системами отсчета. Ведь не следует
забывать, что вводя относительность, релятивисты
особый упор делают на то, что они определяют
метрику пространства по измеримости теми мерами,
которые неподвижны в соответствующей системе
отсчета. И если для одних движений у них одни
меры, а для других движений – другие, то и меры
как таковой в релятивизме уже нет, и после этого
фактически становится бессмысленной вся их
математика.
Другой важный вопрос, поднятый
Вами, которого я хотел бы коснуться здесь, связан
с вашим представлением о том, что в приведенных
мной выкладках используется условие
низкоскоростного предела (v << c). Я уже с одной
стороны показал Вам, что в отличие от
релятивистского варианта, в рассматриваемой
нами задаче не требуется низкоскоростного
ограничения. Но я хотел бы обратить Ваше внимание
еще на один важный аспект вопроса. Релятивисты
при рассмотрении “равноускоренного” движения
не пошли стандартным путем, но исказили и понятие
самого равноускоренного движения. Ответ здесь
очень просто просматривается. Смотрите, в
преобразованиях Лоренца, когда говорят о
невозможности достижения телом скорости выше
скорости света, всегда оперируют выражениями,
полученными в результате преобразований
Лоренца. Но в исходной системе отсчета к скорости
тела прямых ограничений нет. А если релятивисты
оперируют понятием равноускоренного движения в
сопутствующей системе отсчета, то от этого суть
равноускоренного движения не изменяется, и в той
системе отсчета скорость рано или поздно
превысит скорость света. Именно поэтому
релятивисты и уничтожают мгновенно
сопутствующие системы отсчета. Но от этого
ограниченность скорости в релятивистской
концепции не появится, поскольку даже в
выражении для сложения релятивистских
скоростей, в случае однонаправленного движения
тела и подвижной системы отсчета, при достижении
телом в этой подвижной системе скорости света,
получаем |
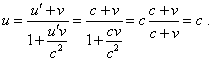 |
(d1.34) |
Как мы видим, в выражении (d1.34)
скорость промежуточной СО v не
регламентируется никакими пределами. Аналогично
мы могли бы зафиксировать скорость
промежуточной системы отсчета, равной скорости
света, и тогда согласно выкладкам, аналогичным
(d1.34), скорость u' или u могла бы
принимать любые значения, большие скорости
света. Наконец, как мы показали в п. 7.1.5 нашей
работы, при встречном движении тела и
промежуточной СО, возможны варианты
значительного превышения скорости света вплоть
до бесконечности, причем с инвертированием
направления движения тела в зависимости от
скорости промежуточной системы отсчета.
Ограничения релятивисты вводят, рассматривая
скорость тела в исходной неподвижной системе
отсчета с точки зрения принятой подвижной
системы отсчета, т.е. путем обратного действия, и
в данном случае ограничения более являются игрой
на той же самой “очевидности”, чем
действительно строгим доказательством того, что
в их концепции скорости, превышающие скорость
света, невозможны. Не зря Эйнштейн, рассматривая
в другой своей работе “О принципе
относительности и его следствиях” возможность
существования относительных движений, больших
скорости света, был уже не столь категоричен: “Скорость v
может принимать любое значение, меньшее c .
Если же W > c , как мы предположили, то v
всегда можно выбрать так, что T < 0 (где T
– время переноса сигнала между двумя точками
системы отсчета – Сергей)” [А.
Эйнштейн, О принципе относительности и его
следствиях, т. 1, с. 76]. Как мы видим, скорость
движущейся системы отсчета следует согласно
мнению Эйнштейна еще и подбирать по величине,
чтобы скорость тела не оказалась большей
скорости света. И то, что Эйнштейн был уверен в
возможности подобного подбора, далеко не
очевидно, поскольку данная скорость задается
условиями задачи и не является предметом
произвольного подбора параметров.
Но с равномерно движущимися
телами просто, поскольку их скорость во времени
не изменяется. С ускоряемыми телами эта самая
“очевидность” уже не срабатывает, поскольку
тело изменяет свою скорость во времени и
требуется не иллюзорное условие предела, а
строгое математическое обоснование, которого в
действительности в релятивистской концепции
нет. Отсутствие этого обоснования обусловлено
тем, что в неподвижной системе отсчета
релятивистская кинематика принимается
идентичной классической. Вот и пришлось
релятивистам в очередной раз пожертвовать
своими постулатами в виде инвариантности
4-инервала, чтобы избежать сверхсветовых
скоростей.
Эта особенность
просматривается в рассматриваемом нами случае.
Граница действительности решения (d1.18)
определяется выражением: |
 |
(d1.35) |
Как видите, никаких ограничений
по малости нет, а до этой границы на основании
преобразований Лоренца тело может ускоряться
без каких-либо препятствий. При этом
единственным аргументом релятивистов может
служить только возможный рост массы. Но здесь они
сами попадают в свой капкан. Ведь они свели
динамику к кинематике, а рост массы может быть
выявлен только в рамках динамики и никак иначе. А
до этого им еще нужно доказать, что законы
сохранения у них соблюдаются при переходе между
инерциальными системами отсчета. В отсутствии
этих доказательств получается, что на границе,
определяемой условием (d1.35), и скорость, и
ускорение тела в подвижной ИСО у них обращается в
бесконечность. Причем этот вывод не
ограничивается малыми скоростями подвижной
системы отсчета и малыми ускорениями. В качестве
иллюстрации, на рис. 5 представлен график
изменения ускорения во времени в подвижной
системе отсчета для разных значений скорости
самой системы отсчета
|
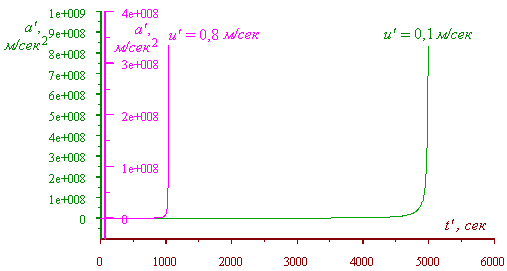
Рис. 5. График изменения
ускорения во времени в подвижной системе отсчета
для разных значений скорости самой системы и
численного значения постоянного ускорения тела
в неподвижной системе отсчета a = 0,001 c,
м/сек2
|
Вы видите, что значения
ускорений достигают своего предела просто в
различные времена, но характер самой функции
сохраняется полностью.
ВЛАДИМИР: Однако, рассматривая
внимательно рис. 3 и рис. 5, обнаруживаю, что a =
0,001c м/сек2 , что вообще
непонятно, т.к. если с – это та с, то
размерность не та. Хотя это тоже близко к
“малым” скоростям, но явно не ньютоновский
предел.
СЕРГЕЙ: Данная запись ускорения
является следствием только удобства в расчетах и
предполагает размерный коэффициент связи, и это
конечно же не связано с релятивистским
представлением ускорения в качестве
безразмерной скалярной величины. Поэтому я везде
оговаривал численное значение. Я точно так же
мог поставить полное значение величины
ускорения, которое оценивалось бы пятизначными
цифрами. Но мне показалось, что сравнение
значения на графике с численным значением
скорости света более впечатляет, учитывая к тому
же, что 10-кратное превышение ускорения над
ускорением свободного падения для человека и
аппаратуры является критическим.
В отношении же ньютоновского
предела вопрос очень расплывчатый, поскольку это
связано с теми погрешностями, которые мы
согласны допустить в расчетах. Иногда важна
точность до пятого-седьмого знака, а иногда и
однопроцентная погрешность избыточна, не так ли?
Значения же я выбирал малыми только исходя из
того, чтобы показать сохранение особенностей
релятивистских искажений при малых значениях
скоростей и ускорений. При больших скоростях и
ускорениях все особенности сохранятся и при
достижении временного предела во всех случаях
скорость и ускорение будут обращаться в
бесконечность. Изменятся только численные
значения параметров.
Если же говорить об интервалах,
вписывающихся в границы скорости света, то
зависимость изменения ускорения во времени
будет иметь несколько иной вид, показанный на
рис. 6.
|
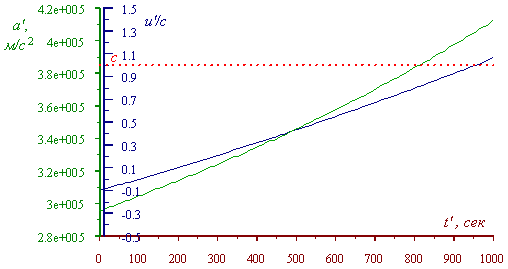
Рис. 6. Совмещенный график
изменения скорости и ускорения тела в подвижной
системе отсчета при равноускоренном движении
тела в неподвижной системе отсчета при v = 0,1 c,
м/сек и численном значении постоянного
ускорения тела в неподвижной системе отсчета a
= 0,001 c, м/сек2
|
Как Вы можете видеть из графика,
если бы релятивистская концепция была
справедлива, то мы не имели бы права применять
понятие равноускоренного движения в нормальном
понимании этого термина даже к тепловым
электронам, находящимся, например, в поле
плоского конденсатора, что немедленно было бы
выявлено в простейших электронных микроскопах и
даже в электронно-лучевых трубках.
ВЛАДИМИР: Получилось весьма
парадоксальное увеличение ускорения a' с
ростом t'. Может быть, это случилось потому,
что кроме параметра (v << c) в решении возник
параметр а t'/v . При этом значения параметра в
силу первого условия не могут значительно
превышать единицу. Так вот, если посмотреть на рис. 3, то легко увидеть,
что рассмотренный в нем диапазон для t'
значительно превышает данное условие. Хотя из
графика видна монотонность функции. Не знаю, что
и сказать. Выполняется ли для Вашего (d1.21) классический
предел?
СЕРГЕЙ: О классическом пределе,
уважаемый Владимир, бессмысленно говорить в
параллель с релятивисткой концепцией.
Существующий классический формализм, как Вы
прекрасно знаете, не обладает данным пределом, и
при развитии этого формализма в область высоких
скоростей ограничение появится без каких-либо
трансформаций пространства и времени и
мифического роста массы, но в результате
корректного учета динамики полей. Динамики! А не
“динамической кинематики”. 
ВЛАДИМИР: По поводу “роста
массы” надо бы разобраться отдельно, уважаемый
Сергей. Очевидно, что всюду в СТО имеется ввиду
инертная ипостась массы. Но далее, в других
разделах теории постулируется
“эквивалентность” гравитационной и инертной
ипостаси массы. А гравитационная ипостась
проявляет себя полем. Со всеми вытекающими. Хотя
вряд ли стоит эту тему развивать именно в этом
диалоге. Возможно, есть смысл рассмотреть её
отдельно.
СЕРГЕЙ: Согласен, и для будущего
диалога будут очень важны те выводы, которые мы
сделаем в этом диалоге, рассматривая
релятивистскую “динамическую кинематику”.
Поэтому продолжим начатую тему, Вы не против? |
Титульная
страница: /1 / 2
/ 3 / 4 / 5 /
|
|







