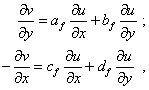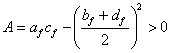101

On complex functions analyticity

On complex functions analyticity

E-mail: selftrans@yandex.ru , selflab@mail.ru

Abstract

We analyse here the conventional definitions of analyticity and differentiability of functions of complex variable. We reveal the possibility to extend the conditions of analyticity and differentiability to the functions implementing the non-conformal mapping. On this basis we formulate more general definitions of analyticity and differentiability covering those conventional. We present some examples of such functions. By the example of a horizontal belt on a plane Z mapped non-conformally onto a crater-like harmonic vortex, we study the pattern of trajectory variation of a body motion in such field in case of a field power function varying in time. We present the technique to solve the problems of such type with the help of dynamical functions of complex variable implementing the analytical non-conformal mapping.

Classification by MSC: 30C62; 30C75; 30C99; 30G30; 32A30; 93A30

Classification by PASC 2001: 02.90.+p; 05.45.-a; 05.45.Ac; 05.45.Jc; 47.32.-y; 47.32.Cc

Keywords: Analytical functions; Theory of complex variable; Dynamical non-conformal mapping; Quasi-conformal mapping; Body trajectory

1. Introduction

In [1] we analysed the ways to find the derivative of the function of complex variable in case when the function does not satisfy the Caushy - Riemann conditions, but is continuous and one-valued in the investigated domain. We showed that the broadening concept of functions differentiability opens new unexpected scope to solve differential equations. However we made no correlation with other classes of functions of complex variable - implementing, e.g., the quasi-conformal mapping. At the same time we should mark that some of the approaches presented in [1] were used before in the formalism of quasi-conformal mapping (see, e.g., [2], [3], [4]). As we will show in this paper, a generalised class of mappings, being one-valued and continuous in the studied domain but not satisfying the Caushy - Riemann conditions, is well wider and can be limited by no specific relationship like Karleman condition. Because in any specific relationship containing an equality, it will be sufficient to change a little the condition, to yield a new class of functions being also one-valued and continuous in the domain of a function, but satisfying neither Caushy - Riemann conditions nor the initial relationship. And up to infinity. To avoid such situation, it is desirable to establish a relationship or a system of relationships whom all classes of such functions will obey, in that number the classes of functions implementing the conformal and quasi-conformal mapping.

2. The limitation of the class of functions implementing the quasi-conformal mapping

Conventionally, the Karleman system

is the basis of quasi-conformal mapping. "The system (1) is the generalisation of Caushy - Riemann conditions (with a = b = c = d = 0  we yield these conditions); some problems of elastic shells, gas dynamics and other sections of continuous media mechanics are reduced to it" [2, p.316].

There is some other concept of such type of mappings, in the form of "a system of the elliptic first-order linear differential equations

where  a_f , b_f , c_f , d_f are the known functions with respect to variable x and y, for which everywhere in the studied domain D   the condition of ellipticity

is true" [2, p.320]. "Compose of the solution u(x,y) and   v(x,y)  of the system (2) a function of complex variable f(z) = u + iv. We will name the mapping that it implements the quasi-conformal mapping connected with this system" [2, p.321].