103

On complex functions analyticity

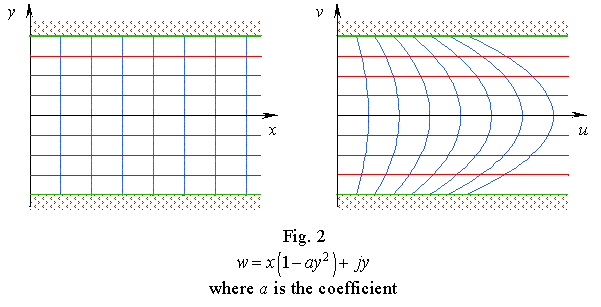
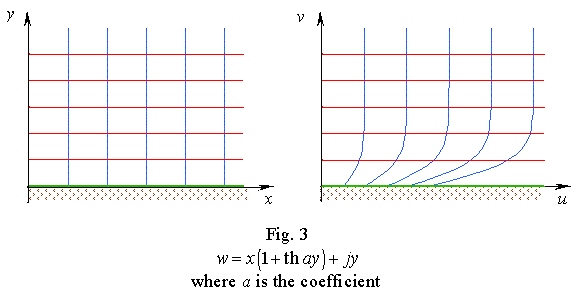
Thus we see that on one hand the studied function (4) satisfies neither conformity nor quasi-conformity conditions. But on the other hand, it maps the infinitesimal circumferences of Z into infinitesimal ellipses of W, which is typical just for quasi-conformal mapping. We can easy generalise this last for the case of any function of a complex variable having continuous first particular derivatives with respect to x and y in the studied point vicinity. It  will suffice to generalise (8) and its obvious transition to (9),  because in the transition to small increments of the function in the point vicinity, we will neglect all powers of an increment higher than the first. Hence, with the finite increment we will always yield the mapping onto the circumference or ellipse. This result is important, as (4) is far from being the only, and the more, it is not an exception from the common rule. To illustrate the said, we show in Figures 2 and 3 two similar functions implementing the mappings of other types. And while in Fig. 2 as a result of mapping the transformation of the entire mapping domain of  W  took place, in Fig. 3 only quite narrow its part transforms, retaining the conformity in the rest part of mapping domain with accuracy to infinitesimal values. The second corollary of the generalisation is that the main theorems of complex function presentation proved for quasi-conformal mapping (see, in particular, [2, pp.316-317]) are applicable in a more general case.

At the same time, this corroborates the statement of introduction that the condition of function analyticity cannot be stated as an equality. This condition can be found only on the basis of some more general principles similar to those which are used when the real-variable functions differentiability was defined. The further studying will be devoted to this.

Definition 1. "The one-valued function f(z) is named analytical (regular, holomorphic) at the point z = a, if it is differentiable in some vicinity of the point a" [5, p.197].

In its turn,

Definition 2. "The function w = f(z) is named differentiable at the point z = a, if the limit

exists at z = a and does not depend on the way in which z tends to zero" [5, p.197, underlined by us - authors].

Note that in the definition of analyticity of a complex-variable function only the requirement, it to be differentiable, is present. The requirement, the limit of (10) to be independent of the way in which z tends to zero, being the basis to derive the Caushy - Riemann conditions (and in the transformed form also the Karleman conditions (1)), appears only in the definition 2. Hence, if some function satisfied the condition that defines the existence of the differential of function and requires this function to be one-valued and continuous in the studied point vicinity, but did not satisfy the condition, the limits of (10) to be equal with  z tending to zero along different directions, then, in the view of basic definition of analyticity, this function is analytical too. It means that both functions studied above and such as

etc., which generally satisfy neither Caushy - Riemann nor Karleman conditions, but have one-valued and continuous derivatives with respect to x and y, are analytical too.