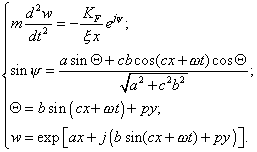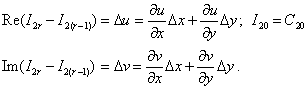108

S.B. Karavashkin and O.N. Karavashkina

Thus, to find the body trajectory within the studied power field, we have to solve the following system of equations:

As we made without any assumptions all pre-conditions which take into account the features of body motion in the studied power field, conveniently solve (23) numerically.

To compose the calculation scheme, divide the studied time interval into a large number n of equal sections t. Then, using the simplest Euler method, integrate the right-hand part of (22) and yield

where _i, x_i, y_i are taken in the beginning of  i-th time interval, in that number x₀, y₀ are the co-ordinates of the prototype of the body initial location at t = 0, and C₁₀ is the integration constant determining the initial velocity of a body.

The second integral over the time we can found the same:

where the constant C₂₀  is determined by the co-ordinates of initial location of the body in the plane W.

In fact, the recurrent relationships (24) and (25) determine the velocity and location of the body in the plane W in the end of each small time interval. To make them working, we have to establish the relation between the prototype and image co-ordinates of the point location in the beginning of each small time interval. Conveniently use the stationary non-conformal mapping (the last expression of (23)). As the selected interval is small, we can write enough accurately:

Passing sequentially the time intervals, at each of them determine the left-hand part of (26), calculating (24) and (25). We can determine the particular derivatives of the right-hand part of the system, differentiating the last expression of the system (26) with respect to x and y and substituting the values, corresponding to the beginning of each time interval. So, solving (26) with respect to   x   and  y, we determine the corresponding shifts of the point prototype and make (24) and (25) recurrent.

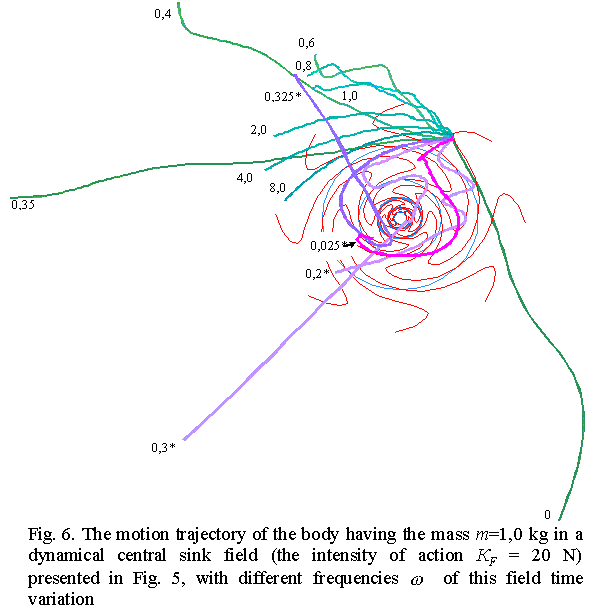
In Fig. 6 we show the body motion trajectories calculated with respect to the field transformation frequency    for the problem stated in the beginning of this item. The initial data for the calculations were taken the following: K_F = 20 N; m =1,0 kg; x₀ = 14 m; y₀ = 0 m; a = 0,2 m^-1; b = /3; c = 1 m^-1; p = /4 m^-1; t₀ = 0 s; t = /1200 s^-1; n = 9600 (four periods of the field time variation). The length of all shown trajectories, except asterisked, corresponds to three periods of the field time variation. To make a visual relation to the field characteristics, we show the initial location of the field equipotential and force lines.

We see that in a stationary power field ( = 0 s^-1) the body moves along the tangent to the line of force on which it located at the initial moment. In the motion the body displaces from the sink axis towards the weak field region; the field action falls and is able only to bend the trajectory insufficiently.

With the time transformation of the field, the trajectory displaces to the sink axis (clockwise), and its length diminishes, but the pattern complicates. The trajectories corresponding to  = 0,2; 0,25; 0,3; 0,325 s^-1have been calculated for four periods of the field variation. At these frequencies, before passing to the field periphery, the body undergoes a few repulsions whose pattern is determined first of all by the field variation frequency. At = 0,2 s^-1 the body moves within a "corridor", being four times repulsed by the lines of force. At  = 0,25 s^-1, after a complicated double repulsion, the body moves along the field equipotential lines, until, repulsing again, it leaves the central domain. At  = 0,3 s^-1 the body first bends around the field centre from the right, then repulses by the lines of force, goes on moving reverse along the equipotential line, repulses again towards the central domain, passes closely near the core and leaves to the periphery from the left of the field centre. And at  = 0,325 s^-1the body moves along the tangent towards the field centre, repulses abruptly towards the centre and leaves to the periphery. However we see that the body is never drawn into the field "crater", which is caused by the non-central pattern of the field action, with the central pattern of the field as a whole. We can expect alike phenomena in other fields, such as an exponential vortex sink.

In the following frequency raising, the trajectory length grows again and the trajectory itself goes on turning clockwise, but only up to  0,4 s^-1. Further the trajectory turns, but the body braking grows (though it already has not a form of repulsions by the lines of force, as it was at the previous band). The trajectory diminishes in length with it. Finally, at frequencies higher than  = 0,6 s^-1, not only the trajectory length diminishes, but it turns reverse. The body first actively responses to the field variation by the small transversal oscillation motions, but as frequency grows, these oscillations smooth and the trajectory smoothly bends the field core along the tangent line.

With diminishing mass, the body motion in a crater-like harmonic field retains its described regularities, though becomes more chaotical and the lines of force repulse the body more often.