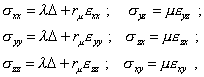17

Волны сжатия в стержне

Особенности распространения продольных волн сжатия в однородном упругом стержне конечного сечения

О.Н. Каравашкина, С.Б. Каравашкин

Специализированная лаборатория фундаментальных исследований СЕЛФ

e-mail: selftrans@yandex.ru , selflab@mail.ru

Эта статья является продолжением обширного цикла, посвященного новой методике получения точных аналитических решений для колеблющихся упругих систем и представляет пример приложения данной методики к практической задаче, на первый взгляд простейшей. Однако даже в этой простейшей задаче точные аналитические решения выявили достаточно серьезные особенности, неизвестные или не учитывавшиеся ранее.

В частности установлено, что в соответствие с динамикой процессов, коэффициент Пуассона должен быть отрицательным, чтобы удлинение стержня соответствовало его утонению и наоборот. Также доказано, что скорость распространения сопутствующих поперечных волн равна скорости продольной волны. И соответственно, скорость сопутствующей продольной волны равна скорости поперечной волны при неравенстве скоростей основных продольной и поперечной волн.

Установлено, что, в рамках линейного моделирования, характер динамического изменения плотности стержня имеет негармонический периодический характер, что существенно расширяет существующий диапазон линейного приближения.

Ключевые слова: Упругие линии с распределёнными параметрами; колебания упругого стержня; поверхностные волны; Линейная система дифференциальных уравнений; коэффициент Пуассона

1. Введение

Задача о линейном моделировании волновых процессов в упругом бесконечном стержне конечного сечения достаточно хорошо известна и является частным случаем более общей задачи о распространении волн в упругих средах с границей. Как известно, "когда имеется граничащая поверхность, могут возникать поверхностные волны. Эти волны, подобные гравитационным волнам в жидкости, были впервые исследованы в 1877 году Рэлеем [1], который показал, что их действие быстро затухает с глубиной и что скорость их распространения меньше скорости волн внутри тела" [2, с.23].

Основой указанного вывода являлось исследование уравнений деформаций в изотропном теле типа

где = _xx + _yy + _zz; и - компоненты Ляме, полностью определяют упругие свойства изотропного тела" [2, с.17].

В частности, для плоской упругой волны в неограниченной изотропной среде, когда перемещение w(w₁, w₂, w₃) зависит только от одной из декартовых координат, например, x, и времени t, предполагается, что в отсутствии массовых сил, "для компонент вектора перемещения w получим следующие уравнения: