т.5 No 2 |
1 |
| Дополнение 1 | |
|
|
т.5 No 2 |
1 |
| Дополнение 1 | |
|
|
Дополнение 1 Уточнение некоторых аспектов анализа концепции чёрных дыр С.Б. Каравашкин, О.Н. КаравашкинаУкраина, 61140, Харьков, проспект Гагарина, 38, кв.187 Тел.: (057) 7370624 e-mail: selftrans@yandex.ru , selflab@mail.ru http://selftrans.narod.ru/SELFlab/index_rus.html http://selftrans.narod.ru/index_rus.html После выхода нашей статьи на нескольких форумах одновременно прошли активные дискуссии. Одновременно с этим, как бы отвечая на наше замечание о сенсациях-однодневках, НАСА выпустило пресс-релиз об открытии её специалистами сразу 21 ЧД, причём достоверность открытия подтвердили несколько известных институтов и лабораторий. В связи с этим мы посчитали необходимым внести ряд уточнений и дополнений в ранее представленное исследование, совместив его с анализом открытия, представленного специалистами НАСА.
Начнём с сомнения одного из коллег, что Эйнштейном в основу ОТО был положен не принцип эквивалентности инерциальной и гравитационной массы, а принцип эквивалентности физических процессов в инерциальных и неинерциальных системах отсчёта. Правда, именно этот вопрос достаточно полно был нами проанализирован на с. 14 работы, причём приведены формулировки и самого Эйнштейна, и его последователей. Все они однозначно утверждают, что под принципом эквивалентности инерциальной и гравитационной масс Эйнштейн подразумевал именно эквивалентность инерционной и неинерционной систем отсчёта. Да и при моделировании релятивистами процессов в полной мере проявляется отражение данного принципа. В частности, когда Ландау выводит метрику Шварцшильда, он прямо указывает на полную свободу замены систем отсчёта вне зависимости от их инерциальности. И это тоже было отражено в нашем исследовании на с. 7. Аналогично Эйнштейн в работе “Проблема частиц в общей теории относительности”, нисколько не задумываясь о физической сути вводимых величин, записывает в решении Шварцшильда новое значение радиуса в виде [1, с. 428] (формула записывается в символах, используемых Шварцшильдом): |
| (1) |
При этом решение Шварцшильда преобразуется к виду |
| (2) |
“Полученные таким
образом новые величины g |
| (3) |
При подобных подходах к
математическому моделированию возможны,
конечно, любые фантасмагорические решения, но
при этом искусственность введения символов
никуда не исчезает и предопределяет последующие
проблемы. С этой точки зрения возникает простой
вопрос: а существует ли в реальности радиус
Шварцшильда в той форме, в которой его описывают
релятивисты, а именно в форме некоторого радиуса R
= Как ни странно может показаться при том обилии литературы, которая издаётся уже более 90 лет и в которой исследуются самые разные варианты геометрии Шварцшильда, при тех обильно финансируемых государственных программах, в рамках которых астрономы пытаются выявить на небосводе объекты, вещество которых сжато до этого радиуса, - ответ на данный вопрос является отрицательным. Действительно, конечное решение Шварцшильда в сферических координатах имеет вид |
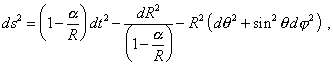 |
(4) |
где R определяется выражением (3). Сингулярность данной метрики, как было сказано выше, имеет место при |
| (5) |
Но R не является измеряемым параметром. Как тоже было уже сказано выше и как следует из постановки задачи в выводе Шварцшильда, измеряемым параметром является r. Поэтому условие (5) в измеряемых параметрах будет иметь вид |
| (6) |
причём из (3) следует, что вследствие неотрицательности измеряемого параметра r должно строго выполняться условие |
| (7) |
Вследствие этого в реально измеряемом параметре сингулярность, как и положено, будет наблюдаться в центре метрики, т.е. в точке расположения гравитирующего тела, и инверсии времени на так называемом горизонте событий (5) не происходит, поскольку с физической точки зрения условие (5) определяет границу области определения параметра R , которая одновременно является и границей справедливости условий моделирования гравитирующего тела физической точкой. Абстрактные же параметры, хоть R , хоть u, абстрактными и останутся. Таким образом, вся широко разрекламированная концепция ЧД является по сути всего лишь следствием некорректного перенесения релятивистами абстрактных решений в реальный мир. При этом и у Эйнштейна, и у Чандрасекара, и у многих других авторов при исследовании сингулярной метрики Шварцшильда уже фигурирует не параметр R , а символ r, вследствие чего в выражениях (1) и (2) нам пришлось менять обозначения на оригинальные по Шварцшильду. Если же не досмотреть данное изменение, а анализировать исключительно развитие мысли, что делает большинство ученых, традиционно доверяющих автору, то виртуальный параметр R исподволь трансформируется в измеряемый параметр r и виртуальный радиус Шварцшильда приобретает видимость реальности, оставаясь по сути столь же абстрактным. И с этим мы напрямую столкнулись при обсуждении нашей работы на форумах. Коллеги так и не смогли понять различие между указанными параметрами с точки зрения прямой их подмены, которая ведёт к подмене действительности виртуальностью. И это закономерно, поскольку заложено в основу релятивистской концепции самими авторами: “Релятивистская теория должна дать ответ на два вопроса: во-первых, какова математическая природа поля и, во-вторых, каким уравнениям должно удовлетворять это поле” [4, с. 725]. Как мы видим, обе цели, обозначенные Эйнштейном, являются парафразами математизации физики, но среди этих целей отсутствует именно та, которая отличает физику от остальных наук - выявление внутренней феноменологической сущности природного явления. Без этой цели, которая должна быть главенствующей в физических исследованиях, сама физика как наука неминуемо выхолащивается в некоторую виртуальную математическую абстракцию, порождающую фантасмагории типа чёрных дыр, воронок времени, фотонных движителей и т.д. Показанная подмена релятивистами реальности виртуальностью подтверждает, что когда в начале основной статьи мы говорили об “особенности” математических подходов релятивистов, мы не преследовали цели опорочить конкретных учёных или концепцию, развиваемую ими, но отражали реальное положение вещей. Чтобы преодолеть указанные проблемы, у релятивистов есть только два пути: или при сохранении формализма существующей концепции построить новую систему ОТО, минуя принцип эквивалентности Эйнштейна и согласовав абстрактные параметры, вводимые ими с измеряемыми, что практически невозможно, - или отказываться от построения, сделанного Эйнштейном, как от ошибочного. Конечно, ни то, ни другое релятивистов не устраивает, но в рамках научной принципиальности третьего варианта, к сожалению, нет. Доказать в рамках корректности физической логики и методологии физики эквивалентность физических законов в ИСО и НСО невозможно, поскольку они неэквивалентны в принципе. |
“Применение неинерциальной системы отсчета определяется характером поставленной задачи… Разумеется, ускорение точки, вызванное неинерциальностью системы отсчета, относительно этой системы вполне реально, несмотря на то, что существуют другие, инерциальные системы отсчета, относительно которых это ускорение отсутствует. В уравнении (для неинерциальной системы отсчета - авт.) ускорение написано так, как если бы оно было обязано некоторым дополнительным силам, которые обычно называют силами инерции. В отличие от сил взаимодействия силы инерции пропорциональны лишь массе каждого тела, к которому они приложены. Это естественно, потому что ускорения, вызванные неинерциальностью системы, по определению одинаковы у тел, помещенных в одну и ту же точку системы и одинаково в ней движущихся. Термин “сила” применен к нему потому, что соответствующие выражения пропорциональны произведению масс на ускорение” [27, с. 75- 76]. И мы в нашей основной работе на примере тела, движущегося относительно свободно падающей НСО, достаточно полно показали эти особенности. К этому можно добавить, что не всегда силы инерции будут реально ощущаться наблюдателем, движение которого рассматривается с точки зрения НСО. В частности, если по отношению к ИСО наблюдатель движется равномерно и прямолинейно, то с точки зрения введенной дополнительно НСО он будет двигаться нелинейно и на него с точки зрения НСО должны действовать некоторые силы инерции. Но на наблюдателя не будут действовать эти силы инерции, хотя при расчетах в НСО их нужно учитывать. И определить эти фиктивные силы можно исключительно, совмещая законы движения в НСО с ИСО. И то, как будут учитываться указанные фиктивные силы, будет зависеть от характера ускорения НСО. Например, в задаче о движении наблюдателя в гравитационном поле с точки зрения НСО, те силы, которые обусловлены взаимодействием наблюдателя с гравитационным полем, будут для наблюдателя реальными. Те же силы, которые обусловлены неинерциальностью самой системы отсчета, будут для наблюдателя фиктивными. Эта ситуация и приводит к тому, что с точки зрения НСО наблюдатель будет сначала притягиваться к гравитирующему центру, а потом как бы отталкиваться. И выявить реальность тех или иных сил можно только, переходя к рассмотрению в ИСО, в которой учитываются только силы, реально действующие на наблюдателя, и не привносятся никакие силы, связанные с нелинейностью движения самой системы отсчета. Именно поэтому в основной статье мы указали, что классическая механика предпочитает инерциальные системы отсчета. “На основании равенства |
| (a) |
легко показать, почему уравнения Ньютона имеют одинаковый вид во всех инерциальных системах отсчета. Силы взаимодействия зависят от относительных координат частиц, и потому они не меняются от преобразования (а), так как общее слагаемое Vt сокращается в аргументе любой функции, содержащей разность координат. В левой части уравнения Ньютона стоят ускорения, т.е. вторые производные координат по времени. Но так как время входит в равенство (а) линейно и в обеих системах по основному предположению одинаково, |
Следовательно, уравнения механики имеют тождественный вид в любых инерциальных системах отсчета. Иначе принято говорить, что уравнения механики инвариантны относительно этих преобразований, называемых обычно преобразованиями Галилея” [27, с. 73]. В неинерциальных системах отсчета подобная инвариантность в общем случае не наблюдается из-за переменного во времени движения самой системы отсчета. |
Содержание / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / Статья