т.5 No 2 |
5 |
| Дополнение 1 | |
|
|
т.5 No 2 |
5 |
| Дополнение 1 | |
|
|
Низвержению Эйнштейном своего второго постулата постоянства скорости света во всех инерциальных системах отсчёта была посвящена ч. 2 нашей работы. Вместе с этим постулатом низвергается и постоянство 4-метрики при переходе к пространству, в котором присутствуют гравитационные поля. И это сам Эйнштейн чётко зафиксировал в своих работах: “Теория относительности формально вытекает из предположения, что для каждого разрешённого преобразования пространственно-временных переменных выражение |
| (13) |
является инвариантом; предположение это вытекает из принципа постоянства скорости света. В соответствии с этим разрешаются только линейные ортогональные преобразования. Уравнение свободно движущейся материальной точки в форме Гамильтона имеет вид |
| (14) |
В случае же отказа от
постулата постоянства скорости света никаких
априорно выделенных систем координат не
существует. Поэтому координаты x |
| (15) |
где величины g |
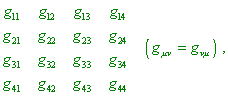 |
(16) |
которые в случае обычной теории относительности (СТО - авт.) соответственно равны |
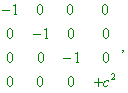 |
(17) |
где c - постоянная. Вырождение такого же рода имеет место в статическом поле тяжести рассмотренного нами типа с тем отличием, что в этом случае g44 = c2 есть функция от x1, x2, x3” [17, с. 231]. Вместе с тем переход от метрики Минковского (13) к обобщённой метрике не столь прост и не ограничивается даже в случае статического гравитационного поля зависимостью четвёртого тензора от пространственных координат. “Из сказанного ранее можно сделать вывод, что между пространственно-временными координатами x1, x2, x3, x4 и результатами измерений, полученными с помощью масштабов и часов, не существует такой простой связи, как в обычной (СТО - авт.) теории относительности. По отношению ко времени это обнаружилось уже для стационарного гравитационного поля” [19, с. 233]. “Именно для того, чтобы выполнялся принцип постоянства скорости света, уравнение |
| (18) |
определяющее распространение света, должно переходить в уравнение |
Отсюда следует, что при некотором выборе системы отсчета должно выполняться соотношение |
| (19) |
где теперь сделана подстановка x1 = x, x2 = y, x3 = z, x4 = ct. Следовательно, система
величин g |
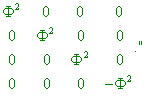 |
(20) |
[20, с. 308]. Нам очень просто проверить это на примере метрики Шварцшильда, которая, как известно, получена была именно для стационарного гравитационного поля точечного источника. В собственных координатах x1, x2, x3, x4 метрика Шварцшильда имеет вид [2, с. 305] |
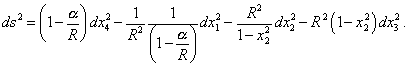 |
(21) |
Матрица, соответствующая этой метрике, имеет вид |
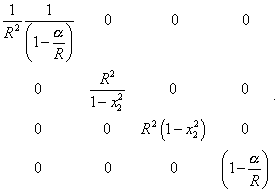 |
(22) |
Из (22) несложно видеть, что даже в случае локального поля, когда R = const, матрица (22) не сводится к (20), а следовательно, принцип постоянства скорости света не сохраняется даже в локальной системе отсчёта, со всеми последствиями для специальной теории относительности. Запись метрики (21) в исходной прямоугольной системе отсчёта будет ещё сложнее и ещё более очевидной в своем несоответствии требованиям локальности, записанным Эйнштейном собственноручно. Если к тому же добавить свидетельства Эйнштейна, признавшего наличие материальных свойств пространства, которые, в частности, приведены нами в ч. 2 основной работы и выше, то отречение Эйнштейна от пустоты пространства как неотъемлемого условия постоянства скорости света во всех системах отсчёта полностью очевидно. В связи с вышеприведенным доказательством отречения Эйнштейна от постулатов СТО, следует привести и доказательство отказа Эйнштейна от введенного им принципа эквивалентности физических законов в инерциальных и неинерциальных системах отсчёта, поскольку это связанные вопросы. Действительно, как мы показали выше, Эйнштейн, переходя от СТО, в которой рассматриваются исключительно инерциальные системы отсчёта, к ОТО, в которой рассматриваются неинерциальные системы отсчёта, отказался от постулата постоянства скорости света. В то же время свет, как известно, является физическим явлением, а его распространение определяется физическими законами. Если согласно Эйнштейну физические законы в неинерциальных и инерциальных системах отсчёта эквивалентны, то скорость света должна оставаться постоянной как в инерциальных, так и в неинерциальных системах отсчёта. Также и метрика Минковского должна сохраняться неизменной независимо от инерциальности системы отсчёта. Если же закономерность распространения света, базовая для релятивистской концепции, нарушается, то и об эквивалентности физических законов в ИСО и НСО говорить бессмысленно. К этому остаётся только добавить, что доказательства, приведенные нами в данном дополнении, не ограничиваются приведенными свидетельствами. Свидетельств очень много, поскольку и СТО, и ОТО постоянно находились в процессе борьбы с вновь и вновь возникающими неразрешимыми противоречиями в фундаменте этих теорий. Это требовало или отказаться от концепций, или делать то, что и делали релятивисты, - а именно, частично отказывались от своих исходных воззрений и представлений, бдительно сохраняя при этом только два основополагающих пункта: инвариантность четырёхмерной метрики и справедливость преобразований Лоренца - т.е. именно то, что является причиной возникающих противоречий. Подобная тактика приводила постоянно к тому, что введенные изменения не только не снимали возникших противоречий, но загоняли их всё больше вглубь проблемы, создавая всё новые и новые противоречия и нестыковки. В принципе, даже того, что показали мы в данном дополнении, не говоря уже о предыдущих наших исследованиях по проблеме Абсолюта [21, с. 308], по эффекту Доплера [22, с. 308], по астрономической аберрации [23, с. 308], вполне достаточно, чтобы признать полное банкротство данного направления, приводящего к тому же к тупиковым моделирующим уравнениям. Но исключительно благодаря тому, что сторонники релятивизма не брезгуют никакими методами в стремлении сохранить свою концепцию, она до сих пор бередит умы учёных, закрывая им действительно перспективные и результативные направления в физике. |
Содержание / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / Статья