СЕЛФ |
6 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
СЕЛФ |
6 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
В этой связи нам хотелось бы коснуться ещё одного вопроса, поднятого на российском Астрофоруме. При обсуждении основной работы, один из коллег полностью отстранил все физические аспекты, поднятые в нашей работе, и сконцентрировал своё внимание на узком вопросе уточнения конкретной математической ошибки, сделанной Шварцшильдом при выводе его конечной формулы (4). При этом к достоинству данного коллеги следует отнести то, что он не ограничился некоторой сомнительной релятивистской литературой, которая в настоящее время публикуется в исключительном обилии, а так же, как и мы, обратился к первоисточнику и правильно уточнил, что в нашем выводе коэффициентов (25)- (30) основной статьи мы не учли условие, записанное Шварцшильдом, при котором будут выполняться полученные нами выражения. Действительно, эти выражения будут выполняться именно в области, бесконечно удалённой от гравитирующего тела, как и указал Шварцшильд. Но и ошибки в выводе Шварцшильда не ограничиваются указанными нами в работе. И если с целью сохранения главной линии нашего исследования мы в работе не акцентировали в полном объеме своё внимание именно на этих чисто математических ошибках, то сейчас в связи с тем, что вопрос об ошибке Шварцшильда поднят принципиально, мы в дополнение к указанной принципиальной математической ошибке, описанной в начале данного дополнения, предложим вниманию читателей те аспекты, которые нами по вышеуказанным причинам были изъяты из конечного варианта исследования. Прежде всего посмотрим на исходное уравнение, на основе которого Шварцшильд развил свой математический аппарат. Это уравнение метрики в прямоугольных координатах [2, с. 201]: |
| (23) |
Чтобы данная метрика удовлетворяла условиям Эйнштейна, она должна сводиться к метрике Минковского в любой локальной области пространства. Причём, поскольку во всех работах по СТО используется именно прямоугольная метрика и инвариантность скорости света должна выполняться в любой инерциальной метрике, то метрика (23) локально должна удовлетворять постулатам СТО. Предполагая это, примем F, G и H постоянными величинами. При этом сразу обратим внимание, что размерность приведенных коэффициентов различна. Если ds имеет размерность в метрах, то F измеряется в метрах2/сек2, G безразмерен, а H имеет размерность 1/метр2. Может ли, например, F быть тоже безразмерным, если ввести скорость света под знак дифференциала по времени? К сожалению, нет. Как мы видели выше, по признанию самого Эйнштейна скорость света в гравитационном поле не остаётся постоянной и зависит от пространственных координат. Поэтому |
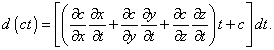 |
(24) |
Из (24) следует, что внося скорость света под дифференциал, мы делаем время зависимым от пространственных параметров. При этом правила дифференцирования, которыми пользовался Шварцшильд в ходе своего вывода, принципиально изменятся и решение будет совсем иным, если вообще оно будет при данных условиях дифференцирования. Здесь сразу необходимо уточнить причины столь сложного дифференцирования. Дело в том, что в общем случае при смещении некоторого пробного тела вдоль траектории ds, в начале и в конце траектории скорость света будет различной. Это естественно повлияет и на дифференциал dt, несмотря на то, что само время впрямую от пространственных координат может и не зависеть. Вследствие этого, если взять параметры положения в начале и в конце бесконечно малого интервала ds и в полном соответствии с правилами нахождения полного дифференциала произвести необходимые операции, то придём к (24). Однако, поскольку Шварцшильд не учитывал зависимость временного параметра от пространственных координат, то и предполагать внесение скорости света под дифференциал мы не имеем права. Идя далее, чтобы осуществить наиболее общую проверку математической правильности решения, мы сравним физическую размерность с конечным решением Шварцшильда и затем пойдём дальше. Конечное значение найденных Шварцшильдом коэффициентов имеет вид |
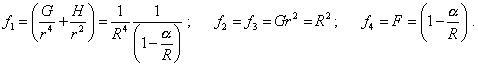 |
(25) |
Из (25) мы сразу видим, что размерность решения для G и H совпадает, а для F нет. Этот параметр безразмерен, что может быть только в том случае, если скорость света находится под дифференциалом, но, как мы показали выше, при этом выкладки будут иметь принципиально иной вид. Таким образом, даже не углубляясь в сами выкладки, можно говорить о некорректности физического вывода в работе Шварцшильда. Далее, рассмотрим исходное выражение (23) с точки зрения удовлетворения локальным условиям СТО. Определитель данной метрики будет иметь вид |
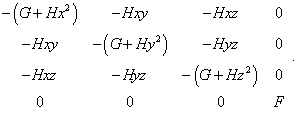 |
(26) |
Из (26) несложно увидеть, что интервал (23) даже в локальном случае постоянного потенциала не сохраняется, изменяясь в зависимости от направленности осей координат, что ставит под сомнение соответствие удобства выбранной Шварцшильдом метрики задачам моделирования. Чтобы показать несоответствие более выпукло, мы можем пойти еще дальше, предполагая вслед за Эйнштейном справедливость СТО в локальных условиях постоянства коэффициентов F, G, H. Для этого предположим, что существует ещё одна (штрихованная) система отсчёта с той же метрикой (23), которая движется вдоль оси x относительно данной системы отсчёта. Если скорость света в локальном смысле в данной метрике сохраняется, то применяя преобразования Лоренца к (23), мы должны прийти к тому же определителю (26). Чтобы реализовать данный переход, мы должны учесть, что в (23) присутствуют как дифференциалы пространственных координат и времени, так и сами координаты. Поэтому мы для облегчения исследования дополнительно должны предположить нулевые начальные условия при интегрировании дифференциальных преобразований Лоренца. При этом указанные преобразования будут иметь вид [24, с. 232]: |
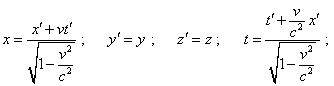 |
(27) |
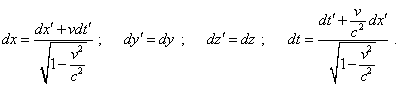 |
(28) |
Подставляя (27) и (28) в (23), получим |
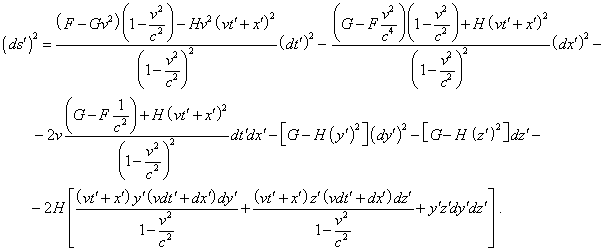 |
(29) |
Сравнивая (29) с (23), несложно по первым трём слагаемым правой части выражения (29) увидеть, что метрики будут эквивалентны исключительно при условии |
| (30) |
т.е. при условии, очень близком к тому, которое мы получили в работе, а именно при условии, что метрика, используемая Шварцшильдом, будет сохранять локальную инвариантность 4-интервала, определённую Эйнштейном, только при условии равенства нулю коэффициента H. И дополнительно, должно быть равенство между G и F / c2. Причём, поскольку выбранная нами локальная область является произвольной, условие (30) должно выполняться во всём пространстве, окружающем гравитирующее тело. При этом определитель метрики приводится автоматически к виду (20), показанному Эйнштейном, а исходное уравнение в выводе Шварцшильда принимает вид |
| (31) |
Данное выражение очень легко переводится в сферические координаты и не нуждается в каких-либо особенных х-координатах, которые придумывал Шварцшильд. Причём (31), а не х-координаты Шварцшильда, будут линейными элементами, которые искал Шварцшильд, определив цель своего исследования следующим образом: “Задача состоит в том, чтобы отыскать линейный элемент с такими коэффициентами, которые удовлетворяли бы уравнениям поля, условию для определителя и четырём перечисленным требованиям (Эйнштейна - авт.)” [2, с. 200]. |
Содержание / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / Статья