SELF |
22 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
22 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
5. The analysis of phenomenological description of entropy The phenomenological description of entropy is connected with the concept of work done on some thermodynamical system. “Unfortunately, the terminology accepted today is not good enough. Actually, the terms ‘work’ and ‘heat’ have double meaning. On one hand, work and heat are two different forms of energy transmission, and on the other they are the quantity of transmitted energy. So in the second case it would be more correct to speak not of the ‘work done’ or of ‘delivered quantity of heat’ but of the energy transmitted, relatively, in the form of work or heat. But to be concise, further, where it will not cause misunderstanding, we will use the conventional terminology, meaning under it the said” [10, p. 193]. Conventionally, “The first law
of energetics is the particular case of the energy conservation law applied to the heat
processes. If the quantity of heat received by the system and expressed by the mechanical
units is |
| (12) |
where (- With it, “we will base the
molecular theory of thermal properties of substance on the following quite natural
assumption: ‘The internal energy of macroscopic body is identical to the average
energy Noting the above aspects, we can see these formulations
limited and applicable only to the local systems where the energy sources are ignored,
even such as chemical energy, nothing to say of global sources. At the same time, in
particular, “chemical
processes are characterised by the transfer of not only the energy but also the substance.
So, considering, for example, an isobaric potential, we have to account that the change of
quantity of moles of some component, in retaining the constant quantity of all other
components and with constant T and p, will change the isobaric potential by
some value. The increment of quantity of chemical energy in the reaction will be expressed
as the product Mathematically, the chemical potentials are the partial derivatives of the characteristic functions with respect to number of moles of the given component of the system at the constant values of independent parameters and quantities of other components: |
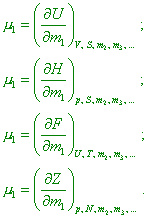 |
(13) |
(where dU, dH, dF and dZ are the increments of interior energy of the system, enthalpy, free energy of the system and isobaric potential relatively – Authors). We can think the chemical potential as the work of chemical forces done in changing of quantity of somewhat component in the system with the constancy of parameters and mass of all other components” [17, p. 26]. With account of this feature, the mathematical record of the first law of energetics (12) also changes. “When the system had n degrees of freedom, we can write the law of energy conservation and transformation as the increment of internal energy of the system equalised to the sum of all n quantities of interaction: |
| (14) |
or through the parameters of state |
| (15) |
[17, p. 16]; here dQ is the change of heat in the system, dA is the work done by the system, and de is the change of sign of the system. It follows from the record of (14) and (15) that there in the thermodynamical system some energy source can be present, and not only local to which the chemical energy relates but also such global as the above considered energy of spontaneous compression of the substance of this system. And Babushkin was correct when wrote the conservation law as (14) expressing the internal energy of the system through all internal and external affecting factors, as these factors change the internal thermodynamical energy of the system and often can have no interrelation with the quantity of heat introduced to the system. Now we already may not represent the temperature in the system as [17, p. 24] |
| (16) |
as, according to (15), the entropy characterises only the change of system’s parameters due to the affection of exterior thermal sources, and the interior energy generally changes under affection of both exterior and interior sources, and the temperature of the system depends on this complex affection. Confining ourselves only to the constancy of volume, as well as writing the first law of energetics in its standard appearance (12), we factually relate the supplied quantity of heat with the full change of the interior energy of the system. So the relation between the change of interior energy and entropy of the system is true only in absence of internal sources that are able to change the thermodynamical balance of the system. But if, as in case with chemical energy, the temperature of system increased either decreased in the reaction and in this connection the done work has changed, the entropy is already unable to account this feature, as it characterises only the change of kinetic energy of the ensemble, due to the heat supply either removal from the system. The same in case of spontaneous gravity compression. As we established, the arising radiation is caused exceptionally by the internal energy of the ensemble of molecules, or rather, by their gravity interaction. In the initial state this does not affect the kinetic energy before the compression begins, but this affects the concentration of density of the energy produced in the compression; we can estimate it, basing on the calculation of regularity of pressure in the homogeneous body which we showed in [18]. |
Contents: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 /