SELF |
26 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
26 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
While the conventional derivation of statistic regularity for entropy does not account this basic aspect that reflects Yavorsky’s refinement [10] (we gave it in the beginning of item 5) that the terms ‘work’ and ‘heat’ have a dual sense: on one hand, it separates these concepts, but at the same time they have much in common, as in both cases this corresponds to a definite quantity of transferred energy. Consequently, in both cases, if the system’s temperature changed, the distribution function and the internal energy of the system change, too. This is natural, although the statistical physicists approach this issue otherwise. “Now consider the change of subsystem’s energy in a more general case, when it interacts with surrounding bodies (medium) and exchanges with them the energy in the immediate contact… As during the whole time of process the system is in equilibrium, the probability distribution is determined by the Gibbs equilibrium distribution (this is why they needed the process to be quasi-static – Authors). For the full change of the average energy, we can write |
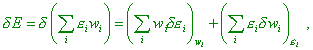 |
(45) |
where wi is the Gibbs distribution with the
temperature equal to that of thermostat, and This last stipulation says, though such separation in variation is formally admissible, the temperature of system is not time-constant, irrespectively of quasi-static pattern of process. While the author interprets the summands in the right part of (45) so: “The first summand in (45) still expresses the work done on the system. The second summand represents the part of energy change of the system interacting with the medium that is not relevant to the change of exterior parameters. In other words, the second summand in (45) is the change of average energy of the system that arises due to immediate energy transfer from the particles of medium to the particles of system, without change of exterior fields either bodies’ relative location. This part of energy change we will call the quantity of heat supplied to the system, denote it dQ. Then |
| (46) |
The formula (46) is the energy conservation law for thermal processes” [11, p. 390]. At the same time, according to the Gibbs distribution law,
wi is the function of |
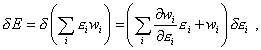 |
(47) |
and in this equality we should not separate the summands into the work of external forces and heat supply, as both summands of the right part of (47) will change in case of some or other way to supply the energy to the system, though in each case in its own way, and we have to determine it in the specific conditions of modelling. Otherwise it appears that for some small quantity of heat |
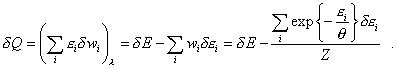 |
(48) |
First of all we see that in (48) the work of external
forces does not turn into zero because of the second term in the right part. Furthermore,
in the second summand of right part of (48), though we vary in |
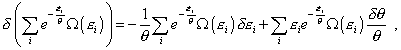 |
(49) |
in which he varies already in the temperature but does not
vary in Nothing of surprise that in the further transformation the author comes to the following expression [11, p. 391]: |
| (50) |
and furthermore, “The formula (50) shows that in a quasi-static process the quantity of heat received either lost by the system can be represented as |
| (51) |
where |
| (52) |
It is obvious that |
| (53) |
where const means an arbitrary
constant. The function Basing on (53), we can easily show the interior
discrepancies that followed from this chain of incorrect operations. Noting that |
| (54) |
Substituting now into (54) the value of energy E
and |
| (55) |
With it, even if we take the work of external forces and the value Q zero, the expression will take the following form: |
| (56) |
and we already may not equalise to zero the second summand in (56), as [11, p. 370] |
| (57) |
and we summate in all states of the system. This means, if at least for one subsystem the probability of existence with higher energy changes in retaining the probabilities for other subsystems, the value Z will inevitably change. Comparing now (57) with (51), we see that even in a particular case, when the work done on the system was absent, these expressions are different. This means, the substitution that the author made in (53) was illegal, nothing to say of his generalisation of the problem, when the difference in definitions increases even more. Thus, we see that the statistic description of entropy, even for ideal thermodynamic systems, is based on the illegal processing the regularities that determine the physical model. Together with the above conclusion of incorrect idea of entropy in nonlinear physical models and models having the internal sources, we can unambiguously conclude: entropy is a fully incorrect concept in thermodynamics, and its generalisation onto macro-scale systems is even more incorrect, as in such systems there are revealed the features ignored in the lab models. |
Contents: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 /