V.6 No 1 |
25 |
| Some improvements to the definition of entropy of macrosystem | |
|
|
V.6 No 1 |
25 |
| Some improvements to the definition of entropy of macrosystem | |
|
|
6. The domain of applicability of the concept ‘entropy’ In the previous item of our study we have cleared up that in fact the area of thermodynamical processes to which the concept ‘entropy’ is applicable is well narrower than it is conventionally thought, and we may not extend it to all natural processes. Under conditions on which the entropy definition is based we have from the very beginning to confine ourselves to an ideal gas or at least to an ideal liquid in small volumes in which the idea of continuous energy as a function of coordinates and pulses in the Gibbs phase space is true. But it appears that the applicability area is even narrower because of the very definition of entropy. “A deeper theoretical analysis allows to establish the basic relationship for thermodynamic applications of the concept ‘entropy’. This relationship interrelates the variation dS of the body’s entropy in the infinitesimal reversible change of its state with the quantity of heat dQ received by the body in this process (we mean, indeed, a non-closed-loop body, so that the reversibility of process does not require its entropy to be constant!). Its shape is |
| (39) |
where T is the body’s temperature. The very fact that dS and dQ are interrelated is quite natural. Heat supply to the body enforces the heat motion of its atoms, i.e. increases their chaotic distribution in different states of microscopic motion, and in this way increases their statistic weight. It is also natural that the influence of given quantity of heat changing the body’s thermal state is characterised by the relative value of this quantity comparing with the full internal energy of the body, so it falls with the growing temperature” [4, p. 214]. Let us draw again our attention that in (39) – which means, in ideal thermodynamic systems, too – the entropy change caused by the energy supplied to the system occurs with the constant temperature, and this is reflected in the denominator of the right part of (39). Usually the scientists try to substantiate it by the quasi-static processes and connect the higher statistic weight of states with the higher energy. But what do they mean under the words ‘quasi–static process’? In particular, “if the exterior parameters were constant (the work of external forces is zero), the energetic levels of the system remain constant (? – Authors). In this case the energy supplied to the system from the outwards is spent to change the distribution of probabilities. The states with higher energy become more probable – the system is heated. If, e.g., the system was an ideal gas, when the energy supply, the number of molecules having relatively more energies increases, and having less energies – decreases. In case if the system gave, not received the energy, there occurs the reverse redistribution of probabilities: the less-energy state becomes more probable, the system is cooled. … Thus, the condition of quasi-static process is its slowness. To each relaxation time relates its own rate of change of exterior conditions at which we can think the process quasi-static” [11, p. 392–393]. In this conventional definition, we see mixed up two strange approaches to the static distribution. On one hand, what it means as such – the static redistribution of energy? Suppose, there is some ensemble of particles. Each particle at some moment of time statistically has some energy. In statistics, the redistribution as such can mean only that at the next moment of time, due to the exchange interactions, the energy of each particle will change, but the curve of static distribution of the system will not change. But if the energies of subsystems change due to the interior energy of the system, there can remain only the general regularity of distribution, but the parameters will be already other, related to the new level of internal energy of each subsystem, – and this will reflect on the energy that the subsystems have at each moment of time and on the parameters of energy distribution in the subsystems of general ensemble. Actually, it is known that after Gibbs, the probability that the ith subsystem of ensemble has the energy wi is |
| (40) |
where “We can think the Gibbs distribution
to be known for some specific physical system, if we know the levels of system’s
energy, i.e. the possible values of the energy Basing on this concept of distribution probability, “consider two subsystems that belong to different systems whose
distribution modules are |
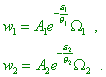 |
(41) |
Premise that both subsystems are driven to a weak interaction, so that they can exchange their energy. Both interacting subsystems can be thought to be a joined subsystem. If this last appears in the state of static equilibrium, the distribution of probability of its states also has to be described by the law like |
| (42) |
On the other hand, as the interaction is weak, we can neglect the interaction energy and think each subsystem quasi-independent. Then to find the distribution of probabilities, we can make use of the theorem of multiplying and write: |
| (43) |
[11, p. 371–372]. With it we may extend (43) also to
macrosystems, because, “when
the subsystem contains so large number of particles that we can think it macroscopic, we
can also speak of its natural statistic temperature. Its temperature is determined from
the equilibrium condition of the system and thermostat and consequently, is equal to the
temperature of this last. To say shortly, we can call Comparing (42) and (43), we can write |
| (44) |
After the thermal equilibrium attained, (44) is true for each subsystem. Hence, when the system’s state changes because of heat transfer, the distribution function changes and with it the internal energies of subsystems change, and their temperatures change, too; this dismays us to represent the heat transfer as the change of distribution function without changing the internal energy of subsystems. |
Contents: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 /