SELF |
24 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
SELF |
24 |
S.B. Karavashkin and O.N. Karavashkina |
|
|
|
Now, basing on the premature results describing the regularities of transformation of elementary volumes in the transformed cloud, we can find the modelling equation of process. We will proceed from the fact that in centrally-symmetric gravity compression, “the attraction force affecting the body moving inside the Earth will be equal to the attraction force created by a sphere with radius equal to the distance from a body to the Earth centre. The value of this force can be determined same as the value of force affecting the bodies located on the Earth’s surface” [20, p. 184]. As the problem is centrally symmetrical, the substance heterogeneity in radius does not change this solution, although some corrects the law of pressure distribution in the depth of gravitating body. Basing on this regularity of internal gravity interaction
and noting the substance redistribution within the cloud, the force affecting the selected
volume |
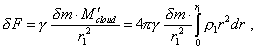 |
(26) |
where r1 is the radius at which the
selected volume |
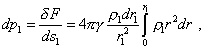 |
(27) |
or in the integral form |
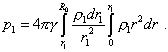 |
(28) |
We see from (28) that the integral in the integrand is taken in limits additional to the limits of major integral, and this complicates the expression. We can surmount it due to the fact that after the substance redistribution, the mass of all selected volumes will remain, which means, the sequence of equalities |
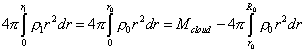 |
(29) |
is true. Furthermore, noting the constant mass of selected volumes, we may write |
| (30) |
Substituting (29) and (30) into (28), yield |
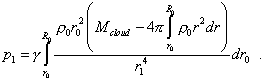 |
(31) |
Finally, noting the adiabatic pattern of process, we may substitute in the left part the pressure by the density, according to (22). So yield |
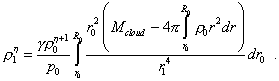 |
(32) |
To pass to the expression for calculation, we have to express r1 through r0 in the denominator of integrand. It is difficult to do it in differential form, as, according to (24), this relation contains the sums in the values of smaller order. But in the finite differences we can do it, premising the small height of selected volumes. First of all, notice that according to the statement of problem, the volumes redistribution in the height with their simultaneous transformation does not cause the change the volume of cloud, hence |
| (33) |
where n is the number of divisions of the cloud radius R0 . It follows from (33) that |
| (34) |
With (34) and (25) we may write the condition of constant mass of selected volume (21) as follows: |
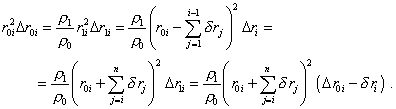 |
(35) |
Thinking the number of divisions to be quite large, we can
neglect in (35) the power of |
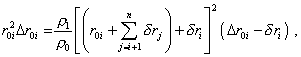 |
(36) |
from which, accurate to the first power of |
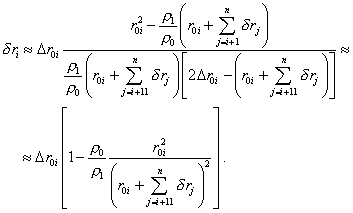 |
(37) |
The yielded expression (37) allows us to determine sequentially the degree of transformation of the elementary volumes of the cloud in its gravity compression. With it, we can take as the starting point of numerical computation the exterior boundary of cloud that is given unchanged. Noting (37), we also can think the relationship (24) defined between r1i and r0i , as above. The calculation scheme will take the form of the system of two equations |
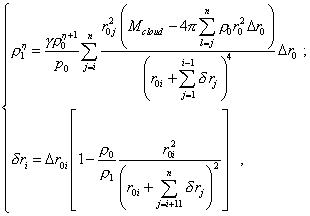 |
(38) |
which is solved by the fitting parameter. The function described by this system of equations is plotted in Fig. 5.
|
Fig. 5. The substance density distribution in the
cloud after the redistribution occurred under affection of the gravity forces. The cloud
mass is Mcloud =10 M
|
This estimating calculation shows, even in a cloud comparably not large in mass, the substance is shrunk from the periphery to the centre. Of course, in a real cloud this process is not so much directed as in the calculation. The interior turbulence will considerably blur the central region; none the less, the temperature there will be by orders higher than that at the periphery, and in large cloud masses – even by dozens and hundreds of orders, which corroborates the possibility of energy self-concentration by way of redistribution under affection of internal gravity forces. At the same time, the calculation shows, the primary concentration of the substance, especially of small astronomic masses, is unable to form a single star. Stars can form only in considerable cloud masses, and not because of primordially shrinking substance but by way of redistribution of local masses of the cloud, due to inevitable internal turbulence of substance within the primordially shrinking cloud. And with insufficiently growing temperature and growing density of substance during the primordial shrinkage, an incomplete star formation is possible (when the temperature of clusters increases to the level of primordial electron cocoons formation but is insufficient to ‘switch on’ the thermonuclear ‘boilers’ at least in one cluster), which would be able to stimulate other clusters. In this case the process is stabilised for quite long term, until it is stimulated by some external processes either by interior turbulence. Then we will see the globules in the clouds, like that shown in Fig. 6.
|
Fig. 6. The globular clusters: the object IC2391. The image was taken by the telescope ROSAT/PSPC in soft X-rays, www.ifa.hawaii.edu/research/stars_and_galaxy.htm
|
Their distinctive feature is the cellar structure with a considerable density of unformed substance between the clusters. Although the described process of stabilisation can have a long duration, the remaining turbulence, with initially weak electron cocoons unable to properly isolate the clusters from each other and from the cloud, will finally cause that at least in one of clusters, by way of joining with others or by redistributed substance, there will appear the conditions initiating the thermonuclear boiler, and it will stimulate the processes in the surrounding objects, which will structurise the cloud into a galaxy. Thus, our numerical calculation showed that in accordance
with known physical laws, there is possible the energy concentration in a local region, by
way of substance redistribution. And as we showed above, with a conventional calculation
technique the entropy of this process will be negative. And here we have to draw the
Reader’s attention, the calculation was conventional. As we could see when modelling,
simultaneously with the cloud’s substance redistribution, the temperature of local
regions will inevitably change, while the entropy means the temperature unchanged. So
logically, we may not consider from the view of entropy concept the processes in which the
energy added either taken away inevitably changes the temperature of system. With it
practically vanishes the physical basis for this parameter, as all physical processes
related to the interior energy change inevitably change the temperature. Only the phase
transition of substance remains that usually is a classical example of entropy process, as
“the phase-to-phase
transition occurs (in the given direction) always at an exact temperature. The ice begins
melting at 0 oC and in further heating the temperature remains constant
up to the moment when all ice turns into water. During this process the ice and water
co-exist in touch with each other” [4,
p. 215–216]. At the same time, from the description of phase transition we see, this
process is essentially nonlinear due to broken bonds, while the very idea of entropy is
applicable exceptionally to linear processes; this makes such application of entropy even
incorrect. The matter is not even, how slowly, how quasi-static will we conduct the phase
transition: it is important that the bonds break in this process, and the slowness does
not matter. Actually, “We can express the entropy of
quasi-closed-loop system through the density of probability From this analysis there follows a natural question: to which physical processes the concept ‘entropy’ is applicable from the view of its phenomenology, if for the systems with interior sources this is invalid, for systems with nonlinear processes of energy supply/removal this concept also losses its sense, and in large-scale ideal gas systems the interactions are revealed which the concept ‘entropy’ is unable to account? |
Contents: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 /