СЕЛФ |
24 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
СЕЛФ |
24 |
| С.Б. Каравашкин и О.Н. Каравашкина | |
|
|
Теперь, основываясь на предварительных результатах, описывающих закономерности трансформации элементарных объемов в трансформирующемся облаке, мы можем найти моделирующее уравнение процесса, исходя из того, что при центрально-симметричном гравитационном сжатии “сила притяжения, действующая на тело, перемещающееся внутри Земли, будет равна силе притяжения, создаваемой шаром радиуса, равного расстоянию тела до центра Земли. Величина этой силы может быть определена точно так же, как и величина силы, действующей на тела, находящиеся на поверхности Земли” [20, с. 184]. Причем, поскольку задача имеет центральную симметрию, то неоднородность вещества по радиусу не изменяет данного решения, хотя и вносит определенные коррективы в закон распределения давления по глубине гравитирующего тела. На базе указанной
закономерности внутреннего гравитационного
взаимодействия и с учетом перераспределения
вещества внутри облака, сила, действующая на
выделенный объем |
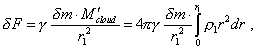 |
(26) |
где r1 - радиус, на
котором расположен выделенный объем |
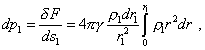 |
(27) |
или в интегральной форме |
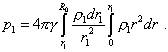 |
(28) |
Из (28) мы видим, что интеграл в подынтегральном выражении берется в пределах, дополнительных к пределам основного интеграла, что усложняет выражение. Но это можно преодолеть, воспользовавшись тем, что в результате перераспределения вещества масса всех выделенных объемов не изменяется, а значит, справедлива цепочка равенств |
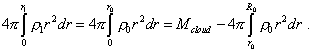 |
(29) |
Кроме того, учитывая опять неизменность массы выделенных объемов, мы можем записать: |
| (30) |
Подставляя (29) и (30) в (28), получим |
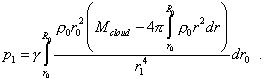 |
(31) |
Наконец, учитывая адиабатический характер процесса, мы можем заменить в левой части давление на плотность в соответствии с (22). В результате получим |
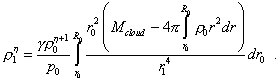 |
(32) |
Чтобы прийти к расчетному выражению, мы должны в знаменателе подынтегрального выражения выразить радиус r1 через r0 . В дифференциальной форме это сделать сложно, поскольку согласно (24), данная связь содержит суммы по величинам более малого порядка. Но в конечных разностях это сделать можно в предположении малой высоты выделенных объемов. Для этого прежде всего учтем, что перераспределение объемов по высоте с одновременной их трансформацией не приводит по условию задачи к изменению общего объема облака, а следовательно, |
| (33) |
где n - число разбиений радиуса облака R0 . Из (33) следует |
| (34) |
С учетом (34) и (25) мы можем записать условие неизменности массы выделенного объема (21) следующим образом: |
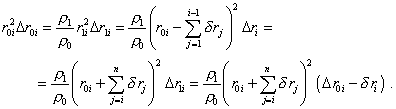 |
(35) |
Считая число разбиений
достаточно большим, мы можем в (35) пренебречь
степенями |
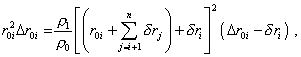 |
(36) |
откуда с точностью до первой
степени |
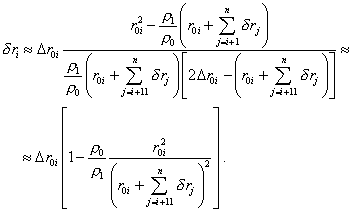 |
(37) |
Полученное нами выражение (37) позволяет последовательно определять степень трансформации элементарных объемов облака при гравитационном сжатии. При этом отправной точкой численных расчетов может стать внешняя граница облака, которая не изменяется по условию задачи. С учетом (37) мы также можем считать определенной связь (24) между r1i и r0i , записанную нами ранее. При этом расчетная схема примет вид системы двух уравнений |
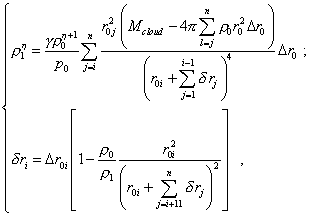 |
(38) |
которая решается методом подбора параметра. Графический вид функции, которая описывается данной системой уравнений, представлен на рис. 5.
|
Рис. 5. График распределения
плотности вещества в облаке после
перераспределения под действием гравитационных
сил. Масса облака Mcloud =10 M
|
Представленный оценочный расчет показывает, что даже в сравнительно небольшом по массе облаке происходит стягивание вещества из периферии к центру. Конечно, в реальном облаке данные процессы не столь однонаправлены, как в представленном расчете. Внутренняя турбулентность будет значительно размывать центральную область, но тем не менее температура в этой области будет выше температуры на периферии на порядки, а в значительных облачных массивах на десятки и даже сотни порядков, что и подтверждает возможность самоконцентрации энергии путем перераспределения вещества под действием внутренних гравитационных сил. Одновременно с этим расчет показывает, что первичная концентрация вещества, и в особенности малых астрономических масс, не способна породить одиночную звезду. Звезды могут образоваться только в значительных облачных массивах, причем не в результате первичного стягивания вещества, а путем вторичного перераспределения локальных масс облака, вследствие неизбежной внутренней турбулентности вещества внутри первично стягивающегося облака. Причем при недостаточном росте температуры и возрастании плотности вещества в ходе первичного стягивания возможно неполное звездообразование (когда температура кластеров поднимается до уровня образования первичных электронных коконов, но недостаточна для зажигания термоядерных котлов хотя бы в одном из кластеров), способное спровоцировать остальные кластеры. В этом случае процесс стабилизируется на достаточно длительное время, пока не будет стимулирован внешними процессами или внутренней турбулентностью. Тогда мы и наблюдаем гранулированные облака, типа приведенного на рис. 6.
|
Рис. 6. Шаровые скопления: объект IC2391, снятый телескопом ROSAT/PSPC в мягких рентгеновских лучах, www.ifa.hawaii.edu/research/stars_and_galaxy.htm
|
Их характерным отличием является ячеистая структура со значительной плотностью несформировавшегося вещества облака между кластерами. При этом описанный процесс стабилизации, хотя и может быть длительным, но сохраняющаяся турбулентность при слабости электронных коконов, не способных в полной мере изолировать сформировавшиеся кластеры друг от друга, выделив их из облака, приведет в конце концов к тому, что хотя бы в одном из кластеров путем объединения с другими, или перераспределения вещества, создадутся условия для зажигания термоядерного котла, который стимулирует процессы в окружающих образованиях, стимулируя структуризацию облака в галактику. Таким образом, представленный
численный расчет продемонстрировал нам, что
согласно известным физическим законам возможна
концентрация энергии в локальной области путем
перераспределения вещества, и как показано нами
ранее, энтропия данного процесса при стандартной
методике расчета будет отрицательной. Причем мы
здесь должны сразу обратить внимание на
сделанный нами акцент по поводу стандартных
расчетов. Ведь, как мы могли видеть в процессе
моделирования, вместе с перераспределением
вещества в облаке неизбежно будет изменяться и
температура локальных областей, в то время как
энтропия предполагает сохранение неизменной
температуры. А следовательно, с чисто логической
точки зрения все процессы, в которых введение или
отведение энергии неминуемо приводит к
изменению температуры физической системы, не
могут рассматриваться с точки зрения понятия
энтропии. Но при этом практически исчезает
физическая база для этого параметра, поскольку
все без исключения физические процессы,
связанные с изменением внутренней энергии,
неминуемо приводят к изменению температуры.
Разве что фазовый переход вещества, который
обычно является классическим примером
энтропийного процесса, поскольку “переход
из одной фазы в другую происходит (при заданном
давлении) всегда при строго определенной
температуре. Так (при атмосферном давлении), лед
начинает плавиться при 0 оС и при
дальнейшем нагревании температура остается
неизменной вплоть до момента, когда весь лед
превратится в воду. В течение этого процесса лед
и вода существуют одновременно, соприкасаясь
друг с другом” [4, с. 215–216]. Вместе с тем, из
самого описания фазового перехода мы видим, что
это существенно нелинейный процесс, связанный с
разрывом связей, в то время как само понятие
энтропии применимо, согласно вышеприведенным
определениям, исключительно к линейным
процессам, что делает данное приложение энтропии
также некорректным. И дело даже не в том, сколь
медленно, т.е. насколько квазистатически, мы
будем осуществлять фазовый переход: важно что в
данном процессе осуществляется разрыв связей и
то, сколь медленно будет это статистически
осуществляться, уже не имеет никакого значения.
Действительно, “Энтропия
квазизамкнутой системы может быть выражена
через плотность вероятности Из данного анализа вытекает естественный вопрос о том, для рассмотрения каких конкретных физических процессов применимо понятие энтропии с точки зрения его феноменологии, если для систем с внутренними источниками это неправомерно, для систем с нелинейными процессами, происходящими при введении/отведении энергии, также это понятие лишается физического смысла, да и в идеальных газовых системах больших масштабов проявляются взаимодействия, которые не учитываются понятием энтропии. |
Содержание: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 /