т.6 No 1 |
25 |
| Уточнения понятия энтропии макросистемы | |
|
|
т.6 No 1 |
25 |
| Уточнения понятия энтропии макросистемы | |
|
|
6. Исследование области применимости понятия энтропии Как мы выяснили в предыдущем пункте исследования, область термодинамических процессов, к которым применимо понятие энтропии, существенно уже, чем обычно её привыкли определять, распространяя на все физические процессы в природе. При тех условиях, которые закладываются в определение энтропии, мы фактически должны с самого начала ограничиться идеальным газом или в крайнем случае идеальной жидкостью малых объемов, в которых действительно справедливо представление о непрерывности энергии как функции координат и импульсов в фазовом пространстве Гиббса. Но оказывается, что указанная область еще уже и это предопределено самим определением энтропии. “Более глубокий теоретический анализ позволяет установить соотношение, являющееся основой для термодинамических применений понятия энтропии. Это соотношение связывает изменение dS энтропии тела при бесконечно малом обратимом изменении его состояния с количеством получаемого им в этом процессе тепла dQ (речь идет при этом, конечно, о незамкнутом теле, так что обратимость процесса не требует постоянства его энтропии!). Оно имеет вид |
| (39) |
где T – температура тела. Самый факт существования связи между dS и dQ вполне естественен. Сообщение телу тепла приводит к усилению теплового движения его атомов, т.е. к увеличению хаотичности их распределения по различным состояниям микроскопического движения, а тем самым к увеличению статистического веса. Естественно также, что влияние заданного количества тепла на изменение теплового состояния тела характеризуется относительной величиной этого количества по сравнению с полной внутренней энергией тела и потому убывает с увеличением его температуры” [4, с. 214]. Опять обратим внимание на тот факт, что в (39), а значит и в идеальных термодинамических системах, изменение энтропии, связанное с подведенной к системе энергией, происходит на фоне постоянства температуры, что отражено в знаменателе правой части (39). Это пытаются обычно обосновать квазистатичностью процессов, связывая с этим повышение статистического веса состояний с большей энергией. Но что при этом понимается под самим квазистатическим процессом? В частности, “если внешние параметры не изменяются (работа внешних сил равна нулю), то энергетические уровни системы остаются неизменными (? – авт.). В этом случае энергия, подводимая в систему извне, идет на изменение распределения вероятностей. Состояния с большей энергией становятся более вероятным – система нагревается. Если, например, система представляет собой идеальный газ, то при подведении энергии число молекул, имеющих относительно большие энергии, увеличивается, а имеющих малые энергии – уменьшается. В случае, если система отдает, а не получает энергию, происходит обратное перераспределение вероятностей: более вероятным становится состояние с меньшей энергией, система охлаждается. … Таким образом, условием квазистатичности процесса является условие его медленности. Каждому времени релаксации отвечает своя быстрота изменения внешних условий, при которых процесс может считаться квазистатическим” [11, с. 392–393]. В данном стандартном определении, как мы видим, переплелись два странных подхода к статистическому распределению. С одной стороны, что значит само по себе статистическое перераспределение энергии? Есть, предположим, некоторый ансамбль частиц. Каждая из частиц статистически в некоторый момент времени обладает некоторой энергией. Перераспределение само по себе в статистике может означать только то, что в следующий момент времени вследствие обменных взаимодействий энергия каждой частицы изменится, но кривая статистического распределения системы не изменится. Если же изменяются энергии подсистем вследствие увеличения внутренней энергии системы, то может сохраниться только общая зависимость распределения, но параметры будут уже другие, соответствующие новому уровню внутренней энергии каждой подсистемы, что отражается и на энергии, которой обладают подсистемы в каждый момент времени и на параметрах распределения энергии по подсистемам общего ансамбля. Действительно, как известно, согласно Гиббсу, вероятность того, что i-я подсистема ансамбля обладает энергией wi , равна |
| (40) |
где “Распределение Гиббса
для какой-либо конкретной физической системы
можно считать известным, если известны уровни
энергии системы, т.е. возможные значения энергии Теперь, основываясь на данном
понятии вероятности распределения, “рассмотрим две
подсистемы, принадлежащие к разным системам,
имеющим модули распределения |
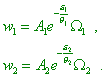 |
(41) |
Предположим, что обе подсистемы приводятся в слабое взаимодействие, так, что между ними может происходить обмен энергией. Обе взаимодействующие подсистемы можно считать объединенной подсистемой. Если последняя оказывается в состоянии статистического равновесия, то распределение вероятностей ее состояний также должно описываться законом вида |
| (42) |
С другой стороны, поскольку взаимодействие является слабым, энергией взаимодействия можно пренебречь и считать каждую из подсистем квазинезависимой. Тогда для нахождения распределения вероятностей можно воспользоваться теоремой умножения и написать: |
| (43) |
[11, с. 371–372]. При этом полученное
выражение (43) мы имеем право распространять и на
макросистемы, поскольку “когда
подсистема содержит настолько большое число
частиц, что ее можно считать макроскопической,
можно также говорить о ее собственной
статистической температуре. Температура ее
определяется из условия равновесия подсистемы и
термостата и, следовательно, равна температуре
последнего. Для краткости можно поэтому называть
Сравнивая (42) и (43), можем записать |
| (44) |
Причем после установления теплового равновесия равенство (44) справедливо для каждой из подсистем. Отсюда следует, что с изменением состояния системы путем передачи тепла, вместе с изменением функции распределения изменяются и внутренние энергии подсистем и их температуры, что не позволяет представить передачу тепла в виде изменения функции распределения без изменения внутренней энергии подсистем. |
Содержание: / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 /