Archivum mathematicum

235 - 236

С.И. Каравашкин

В то же время у Левича [6, с. 107], при исследовании векторного потенциала (, t), создаваемого вдали от диполя с дипольным моментом d (₀), где ₀ - временной параметр, в результате вычислений получается, что

Если подставить (5) в (3), то для того, чтобы даже чисто формально получить выражение (4), необходимо предположить, что одновременно выполняются два равенства. С одной стороны,

а с другой стороны,

В то же время, согласно калибровочной инвариантности, “всегда можно выбрать потенциалы поля так, чтобы скалярный потенциал был равен нулю. Сделать же векторный потенциал равным нулю, вообще говоря, невозможно, так как условие = 0 представляет собой три дополнительных условия (для трех компонент )” [5, с. 73].

Из использования стационарной формы уравнений для дивергенции вектора в системе Максвелла вытекает и проблема избыточности этой системы. Действительно, система уравнений Максвелла для свободного пространства “содержит восемь уравнений для определения только шести неизвестных характеристик электромагнитного поля: E₁ , E₂ , E₃ , H₁ , H₂ , H₃ ” [4, с. 307]. Однако считается, что эта система непротиворечива в связи с тем, “что соотношение

Действительно, если (x, y, z, t) - произвольное дифференцируемое по координатам векторное поле, то div curl = 0 . Поэтому из первого соотношения системы (3) вытекает, что

т.е. div не зависит от времени” [4, с. 307]. Как будет показано ниже, данное утверждение не является доказательством, поскольку дивергенция ротора вектора будет равна нулю и в усовершенствованной теореме о дивергенции вектора. Но главное здесь то, что законы сохранения фактически являются избыточными в том виде, в котором они используются в существующей системе. Например, с существующей точки зрения “условие div = 0 можно рассматривать как условие невозможности появления в пустоте зарядов, если их не было в какой-либо начальный момент времени, а div = 0 - как условие отсутствия магнитных зарядов” [4, с. 307]. И не более. В дальнейшем мы увидим, что в действительности данная пара уравнений Максвелла играет значительно более существенную роль в исследовании динамических процессов в ЕМ поле, а не только “являются существенными ограничениями на дополнительные данные, при которых уравнения Максвелла имеют физический смысл” [4, с. 308].

Вследствие этого мы, имея базовую систему уравнений для исследования динамических полей, в конкретных случаях исследования этих полей должны производить дополнительные операции, приводя модель к квазистационарному виду. В частности, в базовых уравнениях для исследования затухания ЭМ излучения над поверхностью Земли, излучение вертикального диполя представляется в виде [7, с. 130]:

где w(r) - “фактор ослабления”, в котором из известного выражения для бегущей волны изъята временная зависимость и поле излучения рассматривается как стационарное. Это упрощение позволяет выразить “поле в произвольной точке плоскости с помощью функции Грина” [7, с.130].

В некоторых случаях, как, например, при исследовании затухания ЕМ излучения от стационарного источника, различие несущественно, поскольку эту динамическую задачу можно свести к стационарному случаю. Но в ряде задач теории поля, если амплитуда источника будет изменяться во времени, или по характеру исследования необходимо знать мгновенное значение параметров волны в некоторой точке или объеме пространства, то указанное приближение становится некорректным, и необходимо учитывать динамический характер процесса.

Можно привести аналогичные примеры и в области механики. Так, в [8] при выводе стандартного закона сохранения массы в динамическом объеме при исследовании ударной волны в газах, Райхенбах исследует изолированный объем газа V, способный изменяться во времени (V = V(t)) и при этом записывает закон сохранения массы в виде

где d - вектор в направлении внешней нормали к поверхности O объёма V(t), абсолютное значение которого равно величине элемента поверхности … Разделению интеграла на интеграл по объёму и поверхности нетрудно дать физическое объяснение. Первый член в (9) описывает изменение массы внутри объёма во времени (! - авт.), а второй – поток массы через поверхность объёма V ” [8, с. 59]. Понятно, что в выделенном объёме в отсутствии внешних стационарных источников и стоков, масса может изменяться только за счёт наличия разницы между входящим и выходящим потоками. Но при этом теорема Пуассона в форме (1) теряет свою справедливость. Для динамических потоков требуется дополнительно учитывать временной фактор потока.

Это в начале 20 века заметил и Эйхенвальд, исследуя вектор Пойнтинга [9, с. 123]: “если применить уравнение

где f_n - проекция вектора f на наружную нормаль к элементу поверхности ds; W - плотность электромагнитной энергии; - выделенный объем, к конечному объему, то, вообще говоря, правая его часть не будет равна нулю, и электромагнитная энергия внутри данного объема будет меняться со временем”.

Описанная проблема разрешима путем введения соответствия между стандартным определением дивергенции вектора (2) и формулировками теорем, доказываемых на основе этого определения. Следствием введенного соответствия будет в первую очередь реальное обобщение самого определения дивергенции на случай динамических полей. С другой стороны, это позволит связать общим определением дивергенции результаты, получаемые для динамических и стационарных полей. И с третьей стороны, это будет способствовать уточнению методик исследования распространения полей и потоков в пространстве вследствие учета динамического характера процессов.

Описанная задача была поставлена целью исследования, некоторые наиболее важные результаты которого изложены в данной работе.

2. Расчет дивергенции вектора для одномерного динамического ЕМ поля

Исследование дивергенции вектора в динамических ЕМ полях удобно начать с упрощенной модели одномерного потока вектора. Исходя из того, что определение дивергенции “относится к любой векторной функции, а не только к электрическому и гидродинамическому полям, для обозначения этой функции мы будем пользоваться буквой F(x, y, z) ” . Другими словами, “отдадим на некоторое время предпочтение математике перед физикой и будем называть F просто векторной функцией в общем виде, имея в виду, конечно, трехмерное пространство” [10, с. 69].

с. 236

Пусть в некоторой ограниченной связной, свободной от источников и стоков пространственной области   распространяется плоскопараллельная волна, зависимость силового вектора которой (x, t) имеет стандартный вид

где  - частота изменения вектора и   k - волновое число.

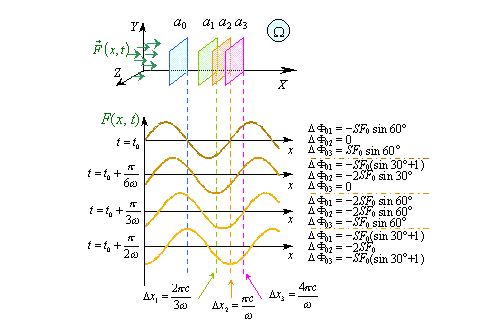
Выделим в данной области четыре площадки a₀, a₁, a₂, a₃ , нормальные к направлению распространения волны, и образуем с их помощью три выделенных объема V₀₁, V₀₂, V₀₃ , ограниченные соответствующими площадками и боковой поверхностью, их соединяющей, как это показано на рис. 1, вверху. При этом, учитывая одномерный характер волны и параллельность (x, t) боковой поверхности выделенных объемов, в дальнейшем рассмотрении боковые поверхности учитываться не будут.

Рис. 1. Диаграмма временной зависимости для исследования потока вектора через выделенный объем

На базе представленной модели и стандартного определения дивергенции вектора (2), определим поток вектора

=

-

= 

, где

Поскольку выделенные нами объемы V₀₁, V₀₂, V₀₃ конечны, то G_i имеет вид