Archivum
mathematicum |
239 - 240 |
| С.И. Каравашкин |

|
с. 239
Следует еще раз отметить, что
именно наличие фазы запаздывания волнового
процесса приводит к тому, что мгновенные
значения амплитуды вектора  (x, t) на
противоположных площадках выделенных объемов
оказываются различными. Из-за этого появляется
зависимость потока вектора от размера
выделенного объема. И это свидетельствует о том,
что при нахождении дивергенции вектора в
динамических полях, в общем случае, необходимо
учитывать временную характеристику потока
вектора. При переходе же к стационарным полям,
т.е. при стандартных условиях стационарности
полей (x, t) на
противоположных площадках выделенных объемов
оказываются различными. Из-за этого появляется
зависимость потока вектора от размера
выделенного объема. И это свидетельствует о том,
что при нахождении дивергенции вектора в
динамических полях, в общем случае, необходимо
учитывать временную характеристику потока
вектора. При переходе же к стационарным полям,
т.е. при стандартных условиях стационарности
полей   0 и/или c 0 и/или c   , правая часть
выражения (17) автоматически обращается в ноль,
тем самым входя в полное соответствие с
существующими представлениями о дивергенции
вектора. , правая часть
выражения (17) автоматически обращается в ноль,
тем самым входя в полное соответствие с
существующими представлениями о дивергенции
вектора.
3. Полное
доказательство теоремы о дивергенции вектора в
динамических полях
Обобщая исследование,
проведенное выше для одномерного потока вектора,
рассмотрим общий случай произвольного потока
вектора  ( ( , t). , t). |

|
(18) |

Рис. 4. Общий вид
трубки потока поля, зависящего от времени
|
Пусть в некоторой связной
однородной области  без источников и стоков распространяется
некоторый поток, вектор которого
без источников и стоков распространяется
некоторый поток, вектор которого  ( ( , t) совпадает с
направлением потока , t) совпадает с
направлением потока  , как
это показано на рис. 4, и зависимость его величины
во времени определяется выражением , как
это показано на рис. 4, и зависимость его величины
во времени определяется выражением
Для нахождения дивергенции
вектора, как и ранее, воспользуемся стандартным
определением (2) и стандартной методикой
определения потока вектора через выделенный
объем, но с учетом фазы запаздывания волнового
процесса в пространстве. Выделим в  некоторый объем V таким образом, чтобы
торцы его совпадали с эквифазными поверхностями
потока, а боковые стороны – с силовыми трубками
тока. Тогда, с учетом конечности скорости
распространения волны, мы имеем право записать некоторый объем V таким образом, чтобы
торцы его совпадали с эквифазными поверхностями
потока, а боковые стороны – с силовыми трубками
тока. Тогда, с учетом конечности скорости
распространения волны, мы имеем право записать |

|
(19) |
где  l –
длина выделенной силовой трубки, l –
длина выделенной силовой трубки,  t - фаза запаздывания
волнового процесса. Таким образом, на основе (19), с
учетом вышерассмотренного частного случая, мы
сразу установили связь между длиной выделенного
объема и фазой запаздывания, и в дальнейшем будем
учитывать этот фактор при проведении
исследования. t - фаза запаздывания
волнового процесса. Таким образом, на основе (19), с
учетом вышерассмотренного частного случая, мы
сразу установили связь между длиной выделенного
объема и фазой запаздывания, и в дальнейшем будем
учитывать этот фактор при проведении
исследования.
Поверхность S , согласно постановке
задачи, состоит из трех составляющих: S = S1 + S2
+ Sl , где S1,
S2 - торцевые поверхности, а Sl - боковая
поверхность выделенного объема. С учетом
постановки задачи и результатов предыдущего
исследования, полный поток через поверхность S
с. 240 |

|
(20) |
где   ( ( , t) = , t) =  ( ( , t) - , t) -  ( ( , t - , t -  t)
. В выражении (20) сразу учтен временной сдвиг
векторной функции, а также отсутствие потока
через боковую поверхность. t)
. В выражении (20) сразу учтен временной сдвиг
векторной функции, а также отсутствие потока
через боковую поверхность.
Первый интеграл суммы (20),
стоящей в правой части, не содержит фазового
сдвига  t . В
рассматриваемом поле без источников и стоков он
обращается в нуль, поскольку в этом случае
становится справедливым условие для дивергенции
векторной функции в стационарных потоках. Второй
интеграл в правой части (20) в общем случае нулю не
равен и может быть легко заменен на интеграл по
объему. Для этого разобьем выделенный объем на p объемов, высота
которых (вдоль линии тока) равна t . В
рассматриваемом поле без источников и стоков он
обращается в нуль, поскольку в этом случае
становится справедливым условие для дивергенции
векторной функции в стационарных потоках. Второй
интеграл в правой части (20) в общем случае нулю не
равен и может быть легко заменен на интеграл по
объему. Для этого разобьем выделенный объем на p объемов, высота
которых (вдоль линии тока) равна |
 |
где p
- любое целое число, большее 1.
После этого подынтегральное
выражение   ( ( , t) можно записать в виде , t) можно записать в виде |

|
(21) |
где  i i ( ( , t) = , t) =  ( ( , t - (i
- 1) , t - (i
- 1) t) - t) -  ( ( , t- i , t- i
 t)
; здесь 1 t)
; здесь 1  i i  p . p .Взяв предел  t t  0 в выражении (21), придем к
интегралу 0 в выражении (21), придем к
интегралу |

|
(22) |
Подставляя (22) в (20) и учитывая,
что, согласно рис. 4, на границе S2   2, а 2, а  2 совпадает с вектором
потока 2 совпадает с вектором
потока  , получим требуемое: , получим требуемое: |

|
(23) |
| Подставляя (23) в (2), придем к
конечному выражению для дивергенции вектора: |
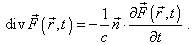
|
(24) |


