5

Решение для конечных упругих линий с сосредоточенными параметрами

ГОМЕЛЬ - ИММС НАНБ - 1999, ТОМ 4, № 3, с. 5-13

МЕХАНИКА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ

УДК 534.1

Точное аналитическое решение задачи о колебаниях в конечной одномерной упругой линии с сосредоточенными массами

С.Б. Каравашкин

Специализированная Лаборатория Фундаментальных Исследований SELF

e-mail: selftrans@yandex.ru , selflab@mail.ru

В статье проанализированы наиболее существенные недостатки существующих подходов к решению задачи о колебаниях в конечной однородной линии с сосредоточенными массами и приведены точные аналитические решения данной задачи для вынужденных и свободных колебаний в конечных линях с незакрепленными концами и с незакрепленным началом и закрепленным концом. Представлен анализ полученных решений и отличие от известных представлений о характере колебаний в рассмотренных линиях. Проведены проверки, подтверждающие полноту и точность решений.

Ключевые слова: математическая физика; волновая физика; динамика; конечные упругие линии с сосредоточенными параметрами; системы обычных  дифференциальных уравнений; микроволновые колебания в упругих линиях

1. Введение

В статье [1] было проведено исследование точных аналитических решений для бесконечных упругих линий с сосредоточенными массами и было показано, что полные аналитические решения, в отличие от известных, содержат в общем случае три режима колебаний: периодический, апериодический и критический. При этом картина колебаний существенно изменяется в зависимости от характера линии (полубесконечная или бесконечная в оба конца), а также и от условий колебаний - т.е. в зависимости от того, являются ли эти колебания вынужденными или свободными (свободными). С конечномерными моделями вопрос обстоит несколько иначе, но, в общем, аналогично. Исследованию данных особенностей и посвящена эта работа.

2. Недостатки существующих методик

Как известно, в настоящее время существует два основных подхода к поиску точных решений задачи о колебаниях в одномерной конечной упругой линии с сосредоточенными массами: это метод разрешенных мод (см., напр., [2] ) и метод Крылова (см., напр., [3], [4], [5] ). Чтобы оценить недостатки указанных методик, проанализируем вкратце каждую из них.

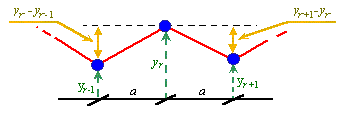
Рис. 1. Расчетная схема

где y_r - вертикальное смещение элементов упругой линии; T - натяжение в линии; m - масса элемента линии; a - расстояние между элементами линии.

Исследование в данном случае проведем по Пейну [2] и относиться оно будет к поперечным колебаниям (см. рис. 1), но суть методики аналогична и для продольных. Решение данной системы уравнений ищется в виде

(где A_r - амплитуда колебаний в линии; - круговая частота воздействующей силы) с граничными условиями для конечной линии с жестко закрепленными концами в виде

Подставляя y_r в исходную систему (1), получают систему алгебраических уравнений типа

которую можно естественно представить в виде системы отношений, постоянной для заданных параметров линии и частоты :